神经网络
神经网络是利用大量节点(神经元)之间的连接关系来进行计算的模型。神经网络的基本结构是由多个神经元组成的网络,每个神经元接收来自其他神经元的输入信号,并产生输出信号。神经网络的学习过程是通过调整神经元之间的连接权重来实现的。
仿生学
神经网络是一种仿生学的模型,它模拟了生物神经元之间的连接方式。在生物神经元中,每个神经元都有一个细胞体,细胞体上有许多树突,树突接收来自其他神经元的信号,然后将信号传递给细胞体。细胞体会根据接收到的信号的强度来决定是否激活,如果激活了,细胞体就会向轴突发送信号。轴突是一个长的细胞突,它会将信号传递给其他神经元的树突。
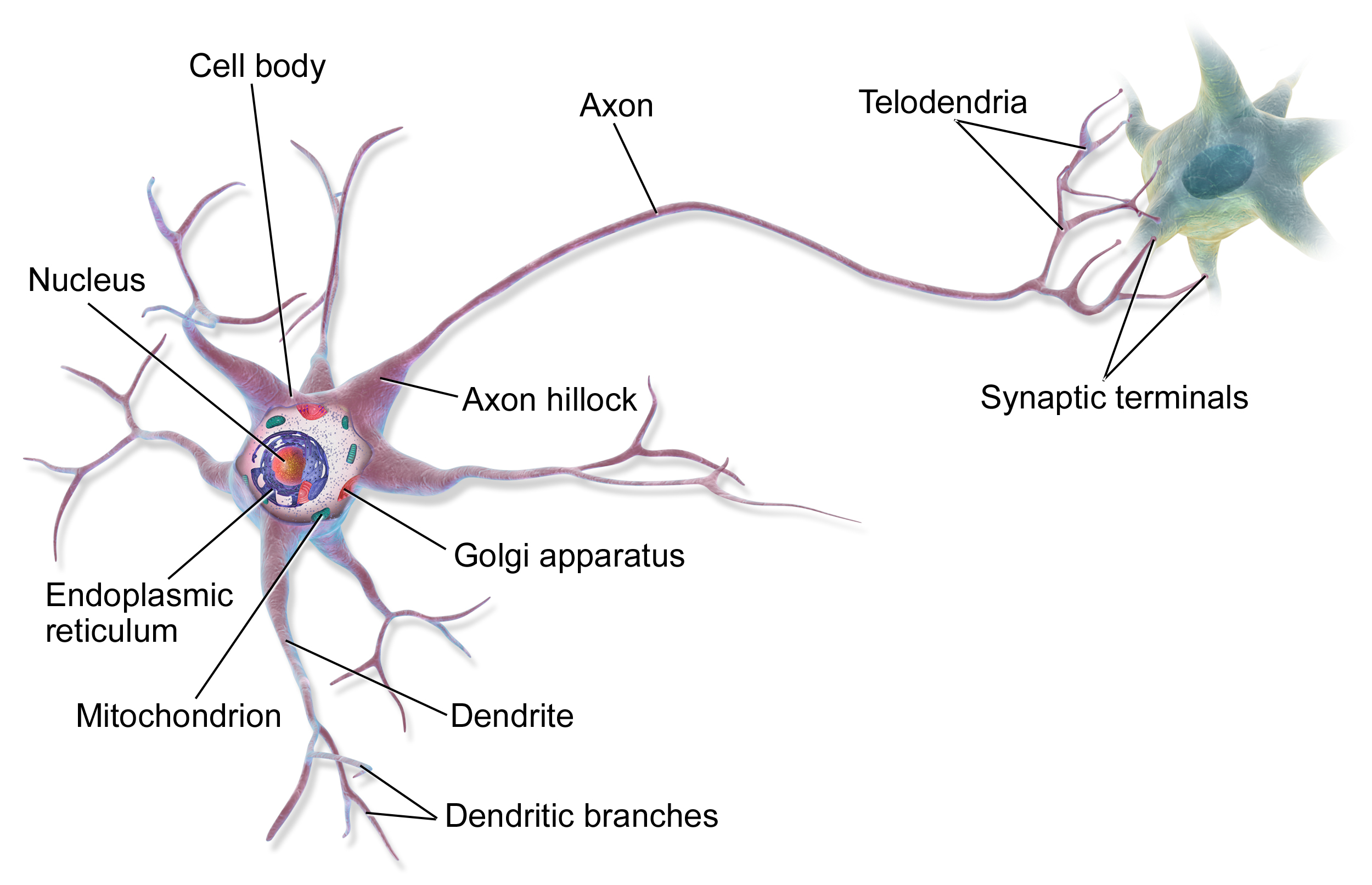
可以带着这个问题思考:神经网络和生物神经元的相似之处在哪里?
MP 神经元的基本结构
对于每个神经元,我们可以用一个 MP 神经元来模拟。MP 神经元的基本结构如下:
- 输入
- 权重
- 激活函数
- 偏置单元
我们可以利用简单的 MP 神经元来实现逻辑运算(使用阶跃函数作为激活函数):
- 与门:令
- 或门:令
- 非门:令
激活函数
激活函数决定了单个神经元的输出。常见的激活函数有:
- 阶跃函数:
- Sigmoid 函数:
这一函数连续、单调,且导数是其本身的函数,满足
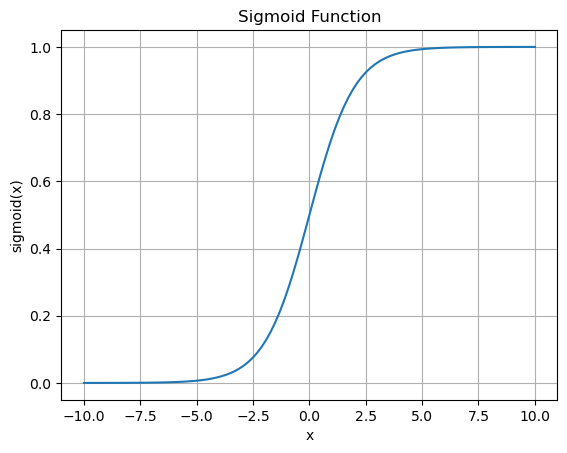
Sigmoid 函数
- Leaky ReLU 函数:
提示
感知机
我们之前介绍过感知机,它类似一个 MP 神经元。可以使用感知机的监督学习机制作为例子,来介绍神经网络的学习机制。我们先来介绍感知机的监督学习的训练机制:
有监督的学习机制
初始化参数:初始化权重向量
循环遍历样本:对于每一个训练样本
判断分类是否正确:如果预测结果
参数更新:对于分类错误的样本
其中,
重复以上过程,直到所有样本都被正确分类或达到设定的迭代次数上限。
虽然感知机可以用于一类分类问题,但是我们发现它无法解决非线性不可分的问题,因为它是单层的,也就是线性的。例如,我们无法用感知机来解决异或问题。
多层前馈神经网络
为了解决感知机无法解决非线性不可分问题的问题,我们引入了多层感知机(MLP)。想象一下,如果将每一层的输出作为下一层的输入,那么我们就可以构建一个多层感知机网络。由于我们的激活函数是非线性的,所以整个网络也是非线性的,这就可以解决一些非线性问题。
一般来说,多层感知机至少包含三层:输入层、隐藏层和输出层。其中,隐藏层可以有多层。这就是一个多层网络。此外,神经元之间不存在同层连接和跨层连接,这就叫做前馈神经网络。一般来说,输入层的神经元个数是与输入数据的维度相同,输出层的神经元个数是与输出数据的维度相同,而隐藏层的神经元个数是可以自由设定的。
多层前馈神经网络的工作原理是:通过前向传播,将输入信号从输入层传递到输出层,计算出输出值;然后通过反向传播,根据输出值和真实值的误差,逐层反向调整神经元的参数,使得误差最小化。可以看出,反向传播借鉴了感知机的监督学习机制。
多层前馈神经网络具有强大的表示能力。已经证明,仅需一个包含足够多神经元的隐藏层,多层前馈神经网络就可以以任意精度逼近任何连续函数
反向传播算法
反向传播算法是迄今为止最常用且最成功的神经网络算法,可以用于多种任务。它是一种基于梯度下降的优化算法,用于调整神经网络的参数,使得网络的输出尽可能接近真实值。
我们给定训练集
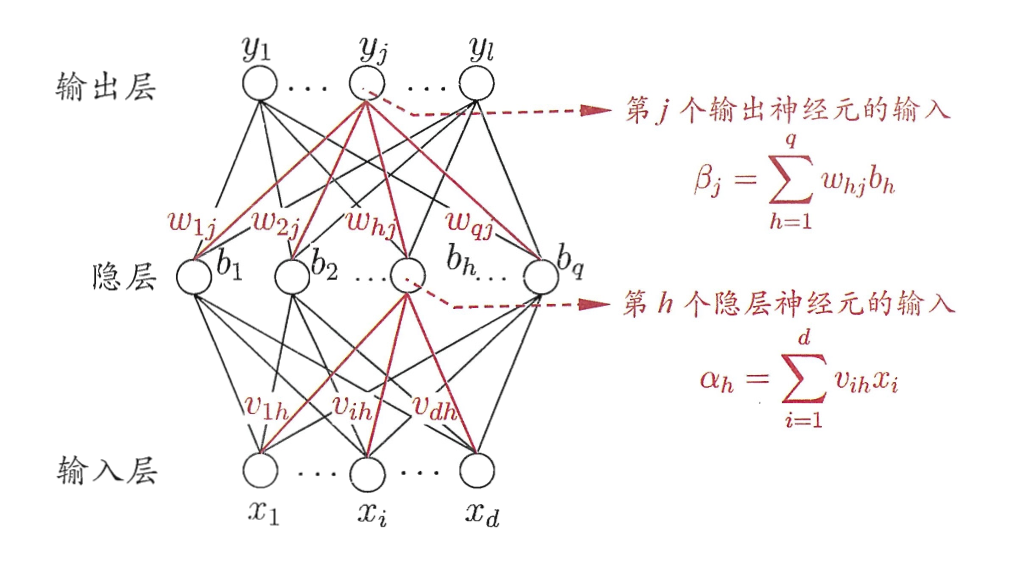
神经网络的示例
对于一个样本
我们首先来解释一下下面使用的各个参数的含义:
对于一个隐藏层参数
其中,
类似地,我们可以下面的公式求出前一层的参数
一般来说,前层参数的修正量需要根据后层参数的修正量来计算,这就是反向传播算法的基本思想。
一个使用 Sigmoid 函数的例子
Sigmoid 函数的导数是
而根据
所以,我们有
可以看出,前层的权重更新信息需要后层的权重更新信息来计算,这也就是反向传播算法的基本依据。
此时,对于这个样本
关于学习率
一般来说,学习率
梯度下降
前文我们了学习率这一概念,它其实就是梯度下降算法中的步长。我们知道,梯度的方向是函数值增加最快的方向,而梯度的反方向就是函数值减小最快的方向。因此,我们可以通过梯度的反方向来调整参数,使得函数值减小。
对于一个函数
- 初始化参数:初始化参数
- 计算梯度:计算函数
- 更新参数:根据梯度的反方向,更新参数
- 重复以上过程,直到满足停止条件。停止条件可以是迭代次数达到上限,或者梯度的范数小于一个阈值。
下面是一个
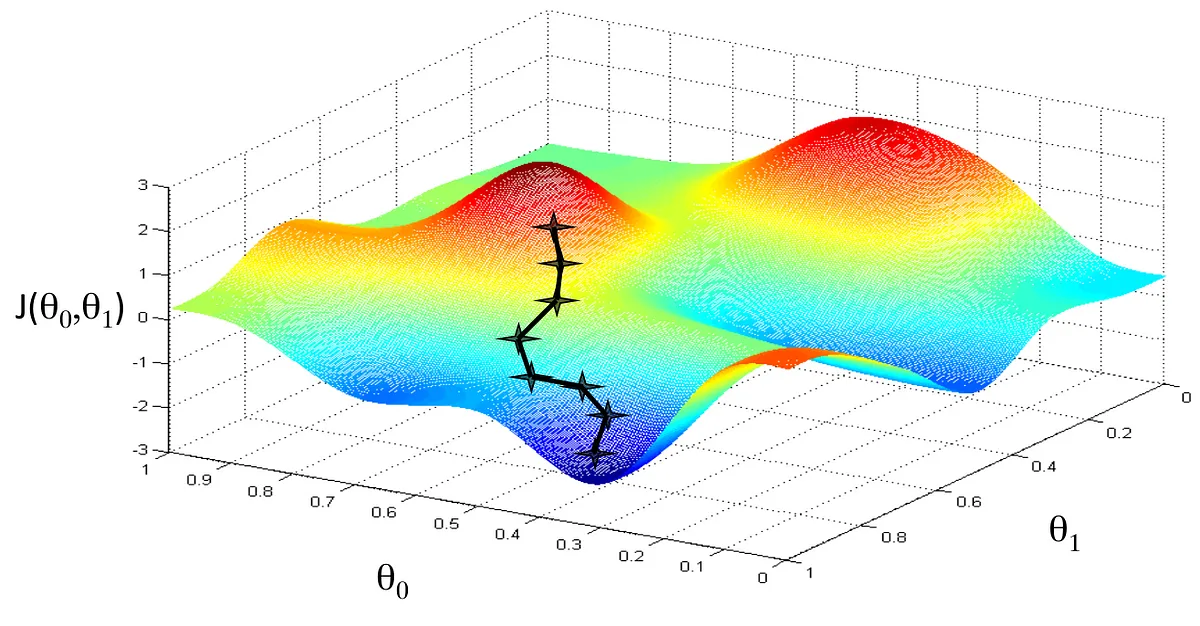
一个梯度减小的示例
可以看出,梯度下降算法没办法保证找到全局最优解,但是可以保证找到局部最优解。所以,我们应当在神经网络中多次随机初始化参数,然后选择最优的参数。
损失函数
分类:交叉熵损失函数
交叉熵是信息论中的一个概念,用于衡量两个概率分布之间的相似度。例如,对于两个概率分布
其中,
相当于衡量 one-hot 的真实标签和预测的各个标签的概率之间的差异。
回归:均方误差损失函数
对于回归问题,我们通常使用经典的均方误差损失函数来衡量网络的输出和真实值之间的差异。对于一个样本
三元组损失
其中,
神经网络的经典模型
TODO
