线性模型

线性可分性

令 $X_0$ 和 $X_1$ 表示 $n$ 维欧式空间的两个点集，如果存在 $n+1$ 个实数 $w_1,w_1,\dots ,w_n,b$，使得对于任意 $X_0$ 中的点 $x$，有 $\sum _{i=1}^n{x}_i{w}_i+b>0$，对于任意 $X_1$ 中的点 $x$，有 $\sum _{i=1}^n{x}_i{w}_i+b<0$，那么称 $X_0$ 和 $X_1$ 是线性可分的。

感知机

感知机由美国学者 $\mathrm{Frank}\mathrm{Rosenblatt}$ 在 $1957$ 年提出，是一种最简单的神经网络模型，是神经网络和支持向量机的基础。它是一个典型的二分类的线性分类模型，也属于判别模型。

即找到一个超平面线性方程 ${\mathbf{w}}^T\mathbf{x}+b=0$，将样本空间划分为两个部分，分别为正类和负类。其中 $\mathbf{w}$ 是法向量，与 $\mathbf{x}$ 的维度相同；$b$ 是位移项，决定了超平面的位置。那么感知机的模型可以表示为（其中 $\mathrm{sign}$ 是符号函数）：

$$f(\mathbf{x})=\mathrm{sign}({\mathbf{w}}^T\mathbf{x}+b)$$

因此，当 ${\mathbf{w}}^T\mathbf{x}+b>0$ 时，$\mathbf{x}$ 被划分为正类；当 ${\mathbf{w}}^T\mathbf{x}+b<0$ 时，$\mathbf{x}$ 被划分为负类。这样，我们就完成了分类工作。

线性模型

试图去学得一个通过属性的线性组合来进行分类的分类函数，其向量形式为 $f(\mathbf{x})={\mathbf{w}}^T\mathbf{x}+b$，其中 $\mathbf{w}$ 和 $b$ 是模型参数。线性模型的特点是简单、基本和可理解性好。但是，线性模型只能适用于线性可分的数据集。

线性回归

线性回归的求解目标是优化参数，使得预测值接近真实值。即优化 $\mathbf{w}$ 和 $b$，使得 ${\mathrm{w}}^{\mathrm{Tx}}+b\approx y$。一个衡量标准是均方误差，即目标是让均方误差最小。对均方误差进行求导，可以得到闭式解。

求导的一个技巧是把所有的样本放在一个矩阵中，矩阵中的每一行都是一个样本，并在矩阵后面加上一列全为 $1$ 的列，记为 $\mathbf{X}$，这样就可以把 $b$ 合并到 $\mathbf{w}$ 中，记为 $\hat{\mathbf{w}}$，如下所示：

$$\mathbf{X}=\left[\begin{array}{ccccc}{x}_{11}& x_{12}& \cdots & x_{1n}& 1\\ x_{21}& x_{22}& \cdots & x_{2n}& 1\\ ⋮& ⋮& \ddots & ⋮& ⋮\\ x_{m1}& x_{m2}& \cdots & x_{mn}& 1\end{array}\right],\hat{\mathbf{w}}=\left[\begin{array}{c}{w}_1\\ w_2\\ ⋮\\ w_n\\ b\end{array}\right]$$

这样，线性回归的目标就变成了优化 $\hat{\mathbf{w}}$，使得 $\mathbf{X}\hat{\mathbf{w}}\approx \mathbf{y}$，其中 $\mathbf{y}$ 是真实值。下面，我们定义损失函数为均方误差（系数 $1/2$ 是为了使求导后的结果简洁），即：

$${\hat{\mathbf{w}}}^{\ast }=\arg \underset{\hat{\mathbf{w}}}{min}\frac{1}{2}||\mathbf{X}\hat{\mathbf{w}}-\mathbf{y}|{|}_2^2$$

对损失函数求导，得到

$$\frac{\partial }{\partial \hat{\mathbf{w}}}(\frac{1}{2}||\mathbf{X}\hat{\mathbf{w}}-\mathbf{y}|{|}^2)={\mathbf{X}}^T(\mathbf{X}\hat{\mathbf{w}}-\mathbf{y})$$

推导过程

设 $E_{\hat{\mathbf{w}}}=\frac{1}{2}||\mathbf{X}\hat{\mathbf{w}}-\mathbf{y}|{|}^2$，我们要求 $E_{\hat{\mathbf{w}}}$ 的最小值，即令 $\frac{\partial E_{\hat{\mathbf{w}}}}{\partial \hat{\mathbf{w}}}=0$。将 $E_{\hat{\mathbf{w}}}$ 展开，我们有：

$$\begin{array}{rl}{E}_{\hat{\mathbf{w}}}& =\frac{1}{2}(\mathbf{X}\hat{\mathbf{w}}-\mathbf{y}{)}^T(\mathbf{X}\hat{\mathbf{w}}-\mathbf{y})\\ & =\frac{1}{2}({\hat{\mathbf{w}}}^T{\mathbf{X}}^T\mathbf{X}\hat{\mathbf{w}}-{\hat{\mathbf{w}}}^T{\mathbf{X}}^T\mathbf{y}-\mathbf{y}\mathbf{X}\hat{\mathbf{w}}+{\mathbf{y}}^T\mathbf{y})\end{array}$$

对 $\hat{\mathbf{w}}$ 求导，我们有：

$$\begin{array}{rl}\frac{\partial E_{\hat{\mathbf{w}}}}{\partial \hat{\mathbf{w}}}& =\frac{1}{2}[({\mathbf{X}}^T\mathbf{X}\hat{\mathbf{w}}+({\mathbf{X}}^T\mathbf{X}{)}^T\hat{\mathbf{w}})-{\mathbf{X}}^T\mathbf{y}-{\mathbf{X}}^T\mathbf{y}]\end{array}$$

这一步我们用到了标量对向量的求导公式，可以参见这篇文章。由于 ${\mathbf{X}}^T\mathbf{X}$ 是对称矩阵，所以 $({\mathbf{X}}^T\mathbf{X}{)}^T={\mathbf{X}}^T\mathbf{X}$，所以我们有：

$$\begin{array}{rl}\frac{\partial E_{\hat{\mathbf{w}}}}{\partial \hat{\mathbf{w}}}& ={\mathbf{X}}^T\mathbf{X}\hat{\mathbf{w}}-{\mathbf{X}}^T\mathbf{y}\\ & ={\mathbf{X}}^T(\mathbf{X}\hat{\mathbf{w}}-\mathbf{y})\end{array}$$

令导数为 $0$，若 ${\mathbf{X}}^T\mathbf{X}$ 正定，则得到闭式解：

$${\hat{\mathbf{w}}}^{\ast }=({\mathbf{X}}^T\mathbf{X}{)}^{-1}{\mathbf{X}}^T\mathbf{y}$$

如果我们令 $\ln y={\mathbf{w}}^T\mathbf{x}+b$，那么线性回归就变成了对数线性回归，在某些情况下，对数线性回归会更加贴近真实的标记。

再者，我们继续推广，令某单调可微的连续函数 $g$，那么线性回归就变成了广义线性回归，其中 $g$ 被称为联系函数。那么，广义线性回归的预测函数为：

$$f(\mathbf{x})=g({\mathbf{w}}^T\mathbf{x}+b)g^{-1}(f(\mathbf{x}))={\mathbf{w}}^T\mathbf{x}+b$$

二分类任务

线性回归模型产生的实值输出的范围可能是 $(-\mathrm{\infty },+\mathrm{\infty })$，而二分类任务的标记是 $0$ 和 $1$。一个简单的想法是利用联系函数 $g$，将实值输出映射到 $[0,1]$ 区间。常用的联系函数有：

• Sigmoid 函数：$g(z)=\frac{1}{1+e^{-z}}$，其中 $z={\mathbf{w}}^T\mathbf{x}+b$；
• 单位阶跃函数：$g(z)=\{\begin{array}{ll}1,& z\ge 0\\ 0.5,& z=0\\ 0,& z<0\end{array}$；

其中，$\mathrm{Sigmoid}$ 函数是一个常用的联系函数，它的导数形式简单，且具有良好的性质。下面我们会继续对它进行开发。

对数几率回归（对率回归）

对数几率回归是一种广义线性回归，它的联系函数正是 $\mathrm{Sigmoid}$ 函数。虽然名字叫做回归，但对率回归其实是一种分类学习方法。并且它不光仅仅输出类别，还会给出近似的概率预测。对数几率回归的模型可以表示为：

$$y=\frac{1}{1+e^{-({\mathbf{w}}^T\mathbf{x}+b)}}$$

根据对数的性质，我们可以得到：

$$\ln \frac{y}{1-y}={\mathbf{w}}^T\mathbf{x}+b$$

将 $\ln \frac{y}{1-y}$ 称为对数几率，它表示了正类的概率与负类的概率之比，即：

$$\ln \frac{p(y=1|\mathbf{x})}{p(y=0|\mathbf{x})}={\mathbf{w}}^T\mathbf{x}+b$$

对数几率回归的损失函数是似然函数的负对数（加一个负号转化为最小化问题），对于数据集 $\{(x_i,y_i){\}}_{i=1}^m$ 即：

$$\begin{array}{rl}\mathcal{L}(\mathbf{w},b)& =-\ln \prod _{i=1}^{m}p(y_i|{\mathbf{x}}_i;\mathbf{w},b)\\ & =-\sum _{i=1}^m\ln p(y_i|{\mathbf{x}}_i;\mathbf{w},b)\end{array}$$

其中，$\mathbf{w},b$ 相当于是参数，而 $p(y_i|{\mathbf{x}}_i;\mathbf{w},b)$ 是对数几率回归预测准确的概率，也就是说，要令每个样本的预测值尽可能接近真实值。关于似然，可以参考另一篇文章。

接下来，我们进一步化简可以得到：

$$\mathcal{l}(\hat{\mathbf{w}})=\sum _{i=1}^m(-y_i{\hat{\mathbf{w}}}^T{\hat{\mathbf{x}}}_i+\ln (1+e^{{\hat{\mathbf{w}}}^T{\hat{\mathbf{x}}}_i}))$$

推导过程

显然，对于似然项，我们可以写成综合两种预测情况的形式：

$$\begin{array}{rl}p(y_i|{\mathbf{x}}_i;\mathbf{w},b)& =p(y_i=1|\hat{\mathbf{x}};\hat{\mathbf{w}}{)}^{y_i}\\ & \times p(y_i=0|\hat{\mathbf{x}};\hat{\mathbf{w}}{)}^{1-y_i}\end{array}$$

那么，代入原式，我们可以得到：

$$\begin{array}{rl}\mathcal{L}(\hat{\mathbf{w}})& =-\ln \prod _{i=1}^{m}p(y_i|{\mathbf{x}}_i;\mathbf{w},b)\\ & =-\sum _{i=1}^m\ln p(y_i|{\mathbf{x}}_i;\mathbf{w},b)\\ & =-\sum _{i=1}^m\ln (p(y_i=1|\hat{\mathbf{x}};\hat{\mathbf{w}}{)}^{y_i}p(y_i=0|\hat{\mathbf{x}};\hat{\mathbf{w}}{)}^{1-y_i})\\ & =-\sum _{i=1}^m[y_i\ln p(y_i=1|\hat{\mathbf{x}};\hat{\mathbf{w}})+(1-y_i)\ln p(y_i=0|\hat{\mathbf{x}};\hat{\mathbf{w}})]\\ & =-\sum _{i=1}^m[y_i\ln \left(\frac{p(y_i=1|\hat{\mathbf{x}};\hat{\mathbf{w}})}{p(y_i=0|\hat{\mathbf{x}};\hat{\mathbf{w}})}\right)+\ln (p(y_i=0|\hat{\mathbf{x}};\hat{\mathbf{w}}))]\\ & =-\sum _{i=1}^m[y_i{\hat{\mathbf{w}}}^T{\hat{\mathbf{x}}}_i-\ln (1+e^{{\hat{\mathbf{w}}}^T{\hat{\mathbf{x}}}_i})]\end{array}$$

最后一步的推导用到了对数几率的定义，即 $\ln \frac{p(y_i=1|\hat{\mathbf{x}};\hat{\mathbf{w}})}{p(y_i=0|\hat{\mathbf{x}};\hat{\mathbf{w}})}={\hat{\mathbf{w}}}^T{\hat{\mathbf{x}}}_i$ 和 $p(y_i=0|\hat{\mathbf{x}};\hat{\mathbf{w}})+p(y_i=1|\hat{\mathbf{x}};\hat{\mathbf{w}})=1$。综合两式就可以得到

$$\begin{array}{r}p(y_i=0|\hat{\mathbf{x}};\hat{\mathbf{w}})=\frac{1}{1+e^{{\hat{\mathbf{w}}}^T{\hat{\mathbf{x}}}_i}}\\ p(y_i=1|\hat{\mathbf{x}};\hat{\mathbf{w}})=\frac{e^{{\hat{\mathbf{w}}}^T{\hat{\mathbf{x}}}_i}}{1+e^{{\hat{\mathbf{w}}}^T{\hat{\mathbf{x}}}_i}}\end{array}$$

在最后一步代入即可。$◻$

线性判别分析

线性判别分析 $\text{(Linear Discriminant Analysis, LDA)}$ 将样例投影到一条直线（或低维空间）上，使得同类样例的投影点尽可能接近，异类样例的投影点尽可能远离。也被称为一种监督降维技术。

例如，给定数据集 $\{(x_i,y_i){\}}_{i=1}^m$，设第 $i$ 类样本的集合为 $X_i$，第 $i$ 类样本的均值为 ${\mu }_i$，第 $i$ 类样本的协方差矩阵为 ${\mathrm{\Sigma }}_i$，那么 $0,1$ 两类样本的中心在直线上的投影点为 ${\mathbf{w}}^T{\mu }_0$ 和 ${\mathbf{w}}^T{\mu }_1$，两类样本的协方差为 ${\mathbf{w}}^T{\mathrm{\Sigma }}_0\mathbf{w}$ 和 ${\mathbf{w}}^T{\mathrm{\Sigma }}_1\mathbf{w}$，那么我们的目标是以下两点：

• 同类样例的投影点尽可能接近，即 ${\mathbf{w}}^T{\mathrm{\Sigma }}_0\mathbf{w}+{\mathbf{w}}^T{\mathrm{\Sigma }}_1\mathbf{w}$ 尽可能小；
• 异类样例的投影点尽可能远离，即 $||{\mathbf{w}}^T{\mu }_0-{\mathbf{w}}^T{\mu }_1|{|}_2^2$ 尽可能大。

推导过程

我们来证明在 $\mathbf{w}$ 下，第 $i$ 类预测的样本投影到直线 $\mathbf{w}$ 后的方差为 ${\mathbf{w}}^T\mathrm{\Sigma }\mathbf{w}$，其中 $\mathrm{\Sigma }$ 是第 $i$ 类样本的协方差矩阵。假设第 $i$ 类样本的集合为 $X$，均值为 $\mu$。

对于投影后的每一个样本 ${\mathbf{x}}_i\in X$ 有 $y_i={\mathbf{w}}^T{\mathbf{x}}_i$ 。那么投影后的样本的均值为 $\tilde{\mu }=\frac{1}{n}\sum _{i=1}^n{y}_i={\mathbf{w}}^T\mu$，方差为：

$$\begin{array}{rl}\mathrm{var}(y)& =\frac{1}{n}\sum _{i=1}^n(y_i-\tilde{\mu }{)}^2\\ & =\frac{1}{n}\sum _{i=1}^n({\mathbf{w}}^T{\mathbf{x}}_i-{\mathbf{w}}^T\mu {)}^2\\ & =\frac{1}{n}\sum _{i=1}^n[{\mathbf{w}}^T({\mathbf{x}}_i-\mu )({\mathbf{x}}_i-\mu {)}^T\mathbf{w}]\\ & ={\mathbf{w}}^T(\frac{1}{n}\sum _{i=1}^n({\mathbf{x}}_i-\mu )({\mathbf{x}}_i-\mu {)}^T)\mathbf{w}\\ & ={\mathbf{w}}^T\mathrm{\Sigma }\mathbf{w}\end{array}$$

对于协方差，可以参考这篇文章。

$◻$

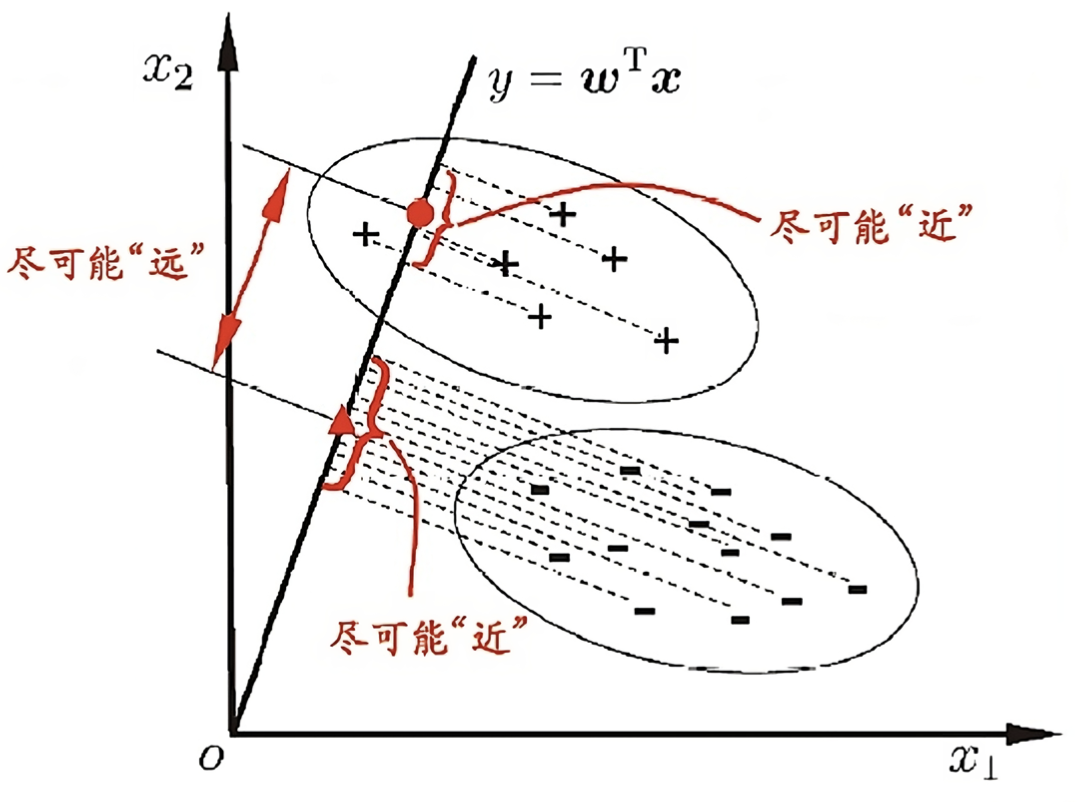
同类接近 异类远离

因此，我们可以定义广义瑞利商：

$$\begin{array}{rl}J(\mathbf{w})& =\frac{||{\mathbf{w}}^T{\mu }_0-{\mathbf{w}}^T{\mu }_1|{|}_2^2}{{\mathbf{w}}^T{\mathrm{\Sigma }}_0\mathbf{w}+{\mathbf{w}}^T{\mathrm{\Sigma }}_1\mathbf{w}}\\ & =\frac{{\mathbf{w}}^T({\mu }_0-{\mu }_1)({\mu }_0-{\mu }_1{)}^T\mathbf{w}}{{\mathbf{w}}^T({\mathrm{\Sigma }}_0+{\mathrm{\Sigma }}_1)\mathbf{w}}\\ & =\frac{{\mathbf{w}}^T{S}_b\mathbf{w}}{{\mathbf{w}}^T{S}_w\mathbf{w}}\end{array}$$

其中，$S_b=({\mu }_0-{\mu }_1)({\mu }_0-{\mu }_1{)}^T$ 是类间散度矩阵，$S_w={\mathrm{\Sigma }}_0+{\mathrm{\Sigma }}_1$ 是类内散度矩阵。显然，它们都是对称矩阵。

对于 $\mathbf{w}$ 而言，我们可以利用拉格朗日乘子法，使得 $J(\mathbf{w})$ 最大化，最后得到 $\mathbf{w}$ 的解为 $S_w^{-1}({\mu }_0-{\mu }_1)$。（在这一模型中，我们只关系 $\mathbf{w}$ 的方向，相当于投影直线的走向）这样，我们就得到了一个闭式解。在实际应用中，通常对 $S_w$ 进行奇异值分解，然后得到 $S_w^{-1}$。

推导过程

由于 $J(\mathbf{w})$ 的分子和分母都是关于 $\mathbf{w}$ 的二次函数，因此结果与 $\mathbf{w}$ 的模长无关（为什么？）。因此，我们不妨固定分母，最大化分子，即

$$\begin{array}{rl}\underset{\mathbf{w}}{min}& -{\mathbf{w}}^T{S}_b\mathbf{w}\\ \text{s.t.}& {\mathbf{w}}^T{S}_w\mathbf{w}=1\end{array}$$

下面我们使用拉格朗日乘子法，定义拉格朗日函数：

$$L(\mathbf{w},\lambda )=-{\mathbf{w}}^T{S}_b\mathbf{w}+\lambda ({\mathbf{w}}^T{S}_w\mathbf{w}-1)$$

对 $\mathbf{w}$ 求导，我们有：

$$\begin{array}{rl}\frac{\partial L}{\partial \mathbf{w}}& =-\frac{\partial ({\mathbf{w}}^T{S}_b\mathbf{w})}{\partial \mathbf{w}}+\lambda \frac{\partial ({\mathbf{w}}^T{S}_w\mathbf{w}-1)}{\partial \mathbf{w}}\\ & =-(S_b+S_b^T)\mathbf{w}+\lambda (S_w+S_w^T)\mathbf{w}\\ & =-2S_b\mathbf{w}+2\lambda S_w\mathbf{w}\end{array}$$

令导数为 $0$，我们有：

$$\begin{array}{rl}{S}_b\mathbf{w}& =\lambda S_w\mathbf{w}\\ ({\mu }_0-{\mu }_1)({\mu }_0-{\mu }_1{)}^T\mathbf{w}& =\lambda S_w\mathbf{w}\\ ({\mu }_0-{\mu }_1)\gamma & =\lambda S_w\mathbf{w}\\ \mathbf{w}& \parallel S_w^{-1}({\mu }_0-{\mu }_1)\end{array}$$

倒数第二步，我们定义 $\gamma =({\mu }_0-{\mu }_1{)}^T\mathbf{w}$，这是一个标量。最后一步，我们就得到了 $\mathbf{w}$ 的方向。$◻$

多分类任务

对于多分类任务，我们可以使用一对多的策略，即将多分类任务转化为多个二分类任务。主要分为两种策略，一种是一对多，另一种是一对一。

• 一对多：对于 $K$ 个类别，我们训练 $K$ 个分类器，第 $i$ 个分类器将第 $i$ 类作为正类，其他类作为负类。在测试时，我们选择分类器输出最高的类别作为预测结果。
• 一对一：对于 $K$ 个类别，我们训练 $C_K^2$ 个分类器，每个分类器只区分两个类别。在测试时，我们选择分类器输出最多的类别作为预测结果。

这两种策略的问题在于类别不平衡，即某些类别的样本数远远大于其他类别的样本数。因此，我们可以使用加权损失函数，即对于每个类别，我们可以设置一个权重，使得每个类别的损失函数对最终的损失函数的贡献相同。（当然，估计类别的权重也比较困难）