Finite Automata

Introduction: What is a Finite Automaton?

Finite automaton is a formal system that remembers only a finite amount of information. A finite automaton has the following components:

• Information is stored in the form of states.
• States changes in response to inputs.
• Rules that tell how the states change in response to inputs are called transitions.

Finite automata are widely used for both design and verification of circuits and communication protocols. It is also used in lexical analysis of programming languages, parsing of programming languages, and pattern matching, which makes it a very important component of compilers.

A brief example: Tennis

Basic rules of tennis in a Game:

• One player serves the ball throughout the game.
• To win a game, a player must win at least four points and be ahead by at least two points.

We can model the game of tennis as a finite automaton. The input to the automaton is the sequence of points won by the two players, we name the input alphabet as $\{s,o\}$ representing the points won by the server and the opponent respectively.

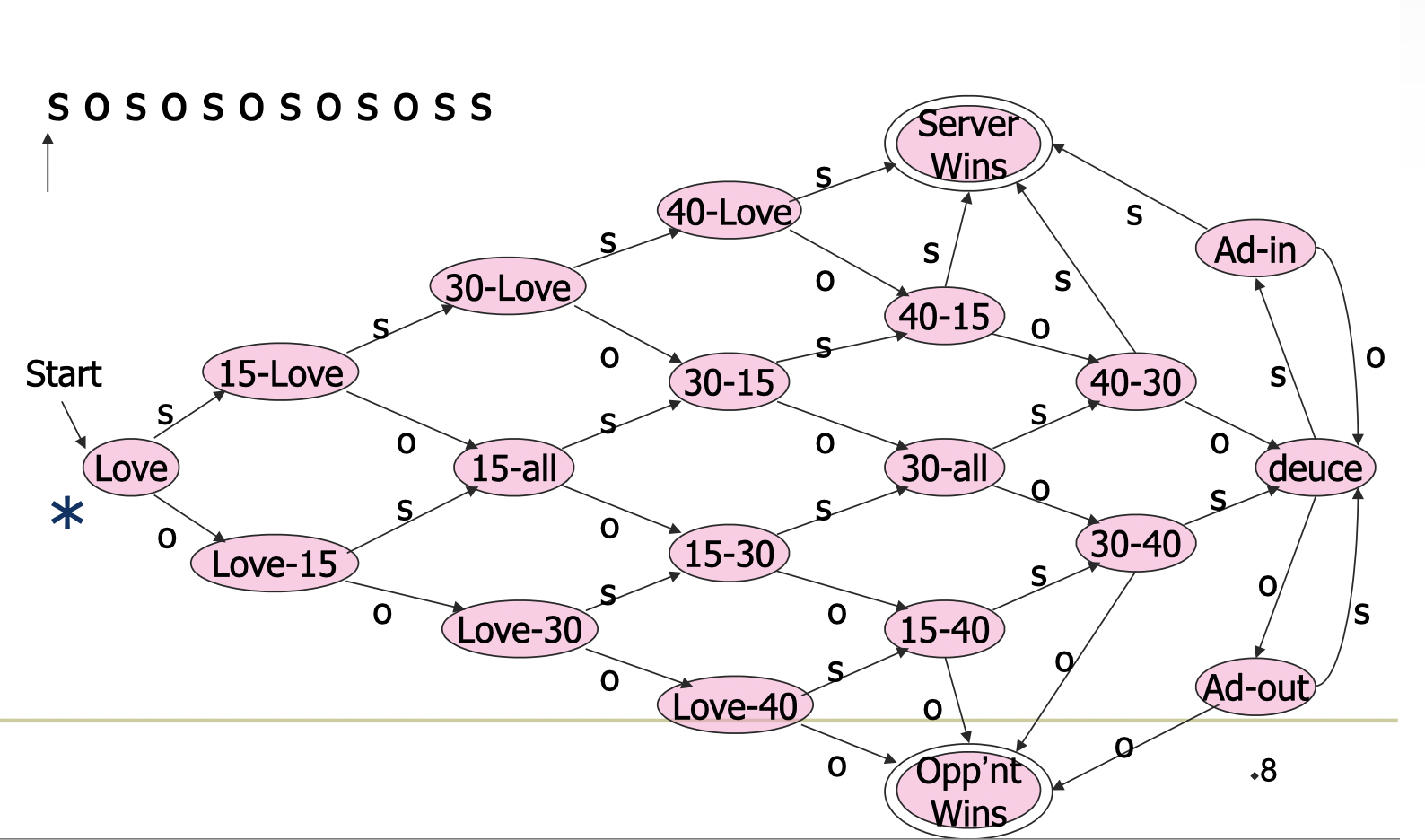
Finite Automaton for Tennis Game

Acceptance of Inputs

Given a sequence of inputs, a finite automaton can either accept or reject the input. The automaton first start in the start state and follows the transitions based on the input sequence. If the automaton reaches one of the accepting states after processing the input, then the input is accepted. Otherwise, the input is rejected.

The set of all inputs that are accepted by the automaton $A$ is called the language of the automaton, which is denoted by $L(A)$.

Deterministic Finite Automaton (DFA)

Preliminary Knowledge: Alphabet, String, Language, Star-Closure, Concatenation, etc.

DFA is a formalism for defining languages, which is consists of the following components:

• A finite set of states $Q$.
• A finite set of input alphabet $\mathrm{\Sigma }$.
• A transition function $\delta :Q\times \mathrm{\Sigma }\to Q$.
• A start state $q_0\in Q$.
• A set of accepting states (final States) $F\subseteq Q$.

Therefore, a DFA can be defined as a 5-tuple $M=⟨Q,\mathrm{\Sigma },\delta ,q_0,F⟩$.

Transition Function

A total function on $Q\times E\to Q$. Let $q\in Q$ be a state and $a\in \sigma$ an alphabet, then $\delta (q,a)=p$ means if the automaton is in state $q$ and reads input $a$, then it will move to state $p$.

Due to the total function, if there is no transition defined for a state and an input, then the automaton will get stuck and reject the input, also known as dropping into a dead state. Once the automaton reaches a dead state, it will never be able to reach an accepting state.

Graphical and Transition Table Representation

DFA can be represented as a directed graph, where the states are represented as nodes and the transitions are represented as edges. The start state is denoted by an incoming arrow and the accepting states are denoted by double circles.

A... Final state?

Final state can also have transitions to some other states. That is, there can be outgoing edges from the final state. So, how to determine if a string is accepted by the DFA?

The string is accepted by the DFA if and only if the automaton reaches an accepting state and the input is completely processed.

Examples of Graphical Representation of DFA:

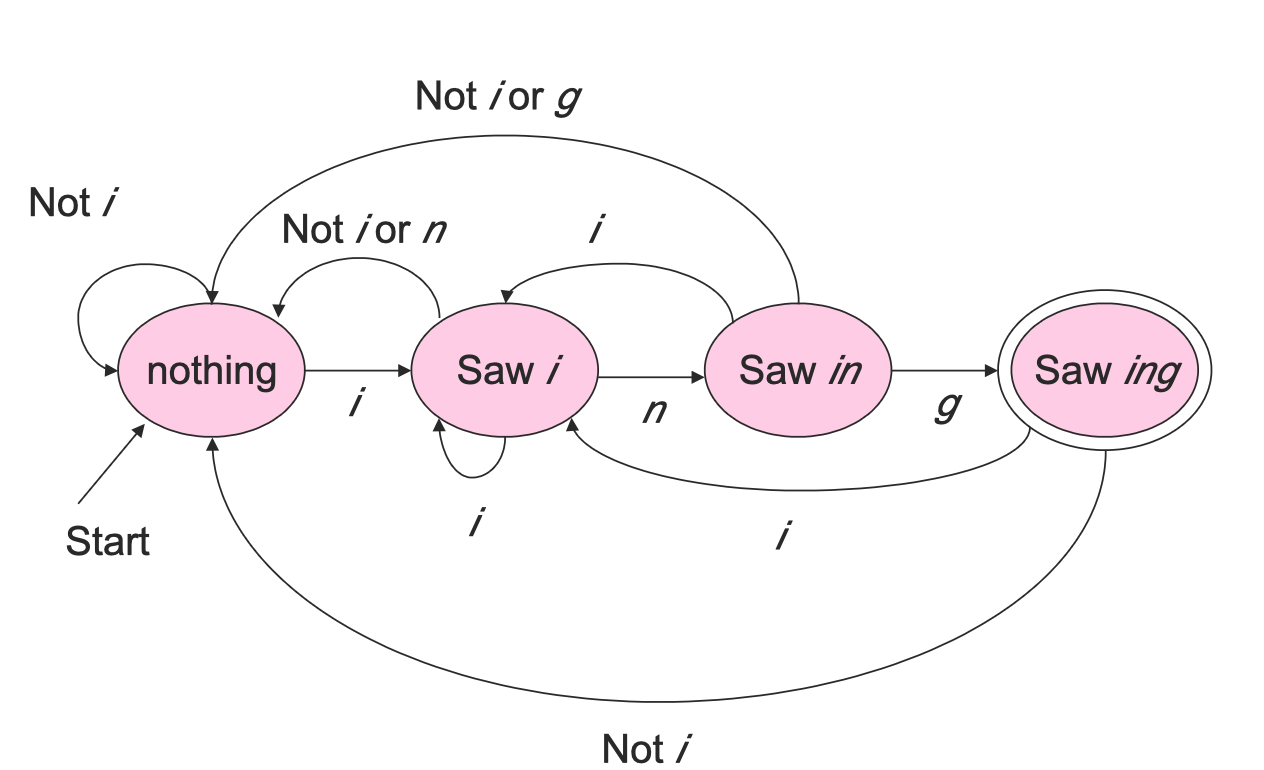
Recognizing String Ending in 'ing'

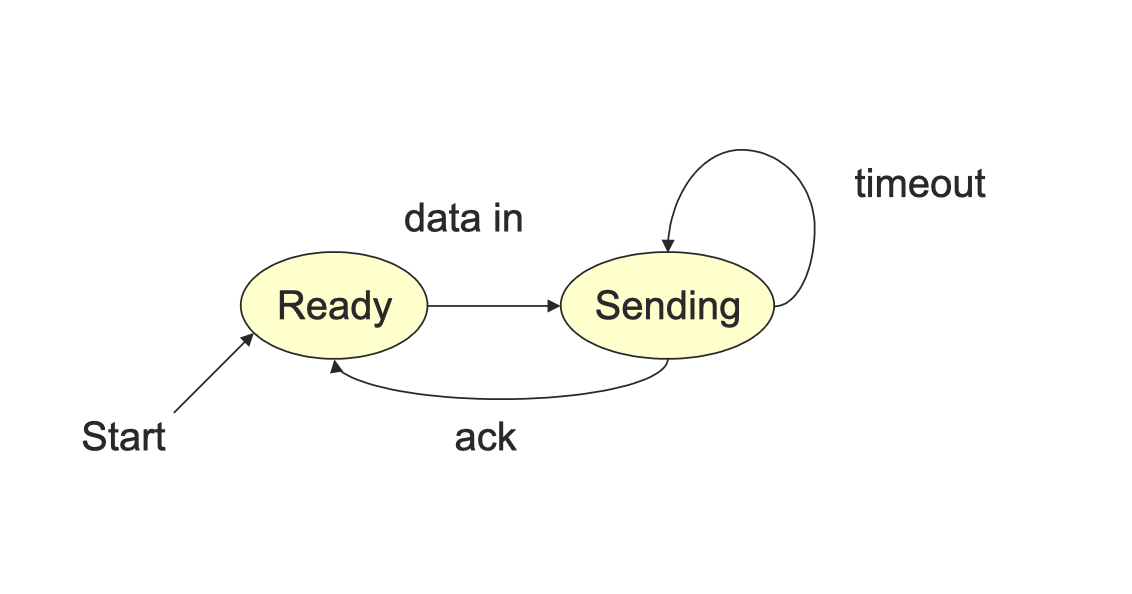
Protocol of Sending Data

DFA can also be represented as a transition table, where the rows represent the states and the columns represent the input alphabet. The transition function is represented as the value in the cell corresponding to the state and input alphabet.

Extended Transition Function

We describe the effect of a string of inputs on a DFA by extending $\delta$ to a state and the string. It is called extended transition function ${\delta }^{\ast }:Q\times {\mathrm{\Sigma }}^{\ast }\to Q$.

By using the extended transition function, we can describe the induction on the length of the string:

• Basis: ${\delta }^{\ast }(q,ϵ)=q$ for all $q\in Q$.
• Induction: ${\delta }^{\ast }(q,xa)=\delta ({\delta }^{\ast }(q,x),a)$ for all $q\in Q$, $x\in {\mathrm{\Sigma }}^{\ast }$, and $a\in \mathrm{\Sigma }$.

Language of a DFA

The language of a DFA $A$ can be formally defined by using the extended transition function as follows:

$$L(A)=\{w\in {\mathrm{\Sigma }}^{\ast }|{\delta }^{\ast }(q_0,w)\in F\}$$

Proof of Language Equivalence

Two DFAs are said to be equivalent if they accept the same language. The usual way to prove the equivalence of two DFAs is to show that their languages are the subset of each other. In order to do that, we often use mathematical induction on the length of the string.

For example, we can prove that the DFA with the language $\{w\in \{0,1{\}}^{\ast }|w{\mathrm{doesn}}^{\prime }\mathrm{t}\mathrm{have}\mathrm{two}\mathrm{consecutive}{1}^{\prime }\mathrm{s}\}$ is equivalent to the DFA with representation as follows:

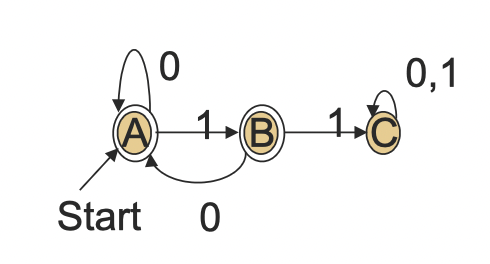
Another DFA's Graphical Representation

Regular Languages

A language $L$ is said to be regular if it is accepted by a DFA. The DFA must accept only the strings in $L$, no others.

Some languages are not regular. For example, the language $\{0^n{1}^n|n\ge 0\}$ is not regular. (Use contradiction and $\mathrm{PHP}$ to prove it.) The finiteness of states in a DFA is the reason why some languages are not regular.

Let us look at some examples of regular languages:

• The language $\{0,1{\}}^{\ast }$, which accepts all strings of 0's and 1's.
• $\{w\in \{0,1{\}}^{\ast }|w,\mathrm{viewed}\mathrm{as}\mathrm{a}\mathrm{binary}\mathrm{number},\mathrm{is}\mathrm{divisible}\mathrm{by}23\}$.