数学基础补充

在机器学习领域中，数学是非常重要的基石，涉及到了代数学、微积分、概率论、统计学等多个分支。相对于传统的系统化的数学学习，机器学习中的数学学习更加注重于应用，因此也就更加分散和颗粒化。可是，从个人的切身体会来看，对于非数学专业的学生或相关人员来讲，如果没有系统地学习过这些数学分支，这些知识可能看起来并没有那么“基础”。这样看来，我们可以以机器学习的视角出发，快速地填补一些知识漏洞，或者去重温这些数学知识。这篇文章的目标就是集中地整理机器学习中所涉及的数学基础知识。全文以知识点的方式布局，并且假定读者已经具备了大学本科层次的高等数学和线性代数的基础知识（即绝大多数理工科专业数学基础课程的知识）。

矩阵的导数

这一部分不需太纠结，能理解公式的意义即可。

在高等数学中，我们学过一元函数 $f(x)$ 的导数的定义，同时也学过多元函数如 $u(x,y)$ 的偏导数的定义。这些导数，我们可以统称为标量对标量的导数，因为无论自变量如何，极限式的分子分母始终都是一个数值。

我们在线性代数中还学过向量和矩阵。在实际应用中我们发现，很多运算都可以简记为向量和矩阵的形式，并且它们还有一些良好的性质来方便我们计算。那么，导数的概念是否可以继续推广呢？先来看一个简单的例子。

符号说明

• 用大写粗体字母表示矩阵，如 $\mathbf{A}$；用斜体字母和脚标表示矩阵中的元素，如 $A_{ij}$ 或 $a_{ij}$；
• 用小写粗体字母表示向量，如 $\mathbf{x}$；用小写斜体字母和脚标表示向量中的元素，如 $x_i$；如没有特殊说明，约定向量为列向量；
• 用小写斜体字母表示标量，如 $f$ 或 $x$。

对于随机变量：

• 单一的随机变量用大写斜体字母表示，如 $X$；对于随机变量的取值，我们用小写斜体字母表示，如 $x$；
• 随机变量组成的向量，我们用大写粗体字母加向量上标表示，如 $\overrightarrow{\mathbf{X}}$；用大写斜体字母和脚标表示向量中的元素，如 $X_i$；
• 随机变量组成的矩阵，我们直接用大写粗体字母表示，如 $\mathbf{X}$；用大写斜体字母和脚标表示矩阵中的元素，如 $X_{ij}$。

梯度 梯度是一个向量，表示某一多元函数在该点处的方向导数沿着该方向取得最大值。对于一个具有一阶连续偏导数的多元函数 $f(\mathbf{x})$（这里，我们把自变量看作一个向量，这也是在机器学习中的惯用做法），我们知道在 ${\mathbf{x}}_0=(x_1,x_2,\cdots ,x_n{)}^T$ 处的梯度为：

$$\mathrm{\nabla }f(\mathbf{x})={[\frac{\partial f}{\partial x_1},\frac{\partial f}{\partial x_2},\cdots ,\frac{\partial f}{\partial x_n}]}^T$$

这里，$\mathrm{\nabla }$ 是梯度算子，$\mathrm{\nabla }f(\mathbf{x})$ 是 $f(\mathbf{x})$ 的梯度。梯度的每一个分量都是 $f(\mathbf{x})$ 对应的自变量的偏导数。这样，我们不妨把标量对标量的导数推广到标量对向量的导数。定义

$$\frac{\partial f}{\partial \mathbf{x}}={[\frac{\partial f}{\partial x_1},\frac{\partial f}{\partial x_2},\cdots ,\frac{\partial f}{\partial x_n}]}^T$$

这样，我们就可以把梯度的公式简写为

$$\mathrm{\nabla }f(\mathbf{x})=\frac{\partial f}{\partial \mathbf{x}}$$

由此我们可以看出，向量和矩阵的求导其实就是对多元函数求偏导，只不过是将自变量、因变量和结果排列成了向量或矩阵的形式，是一种简记的方式。当然，在我们全部定义后，它还可以推出很多方便的性质可用于推导和计算。这就是矩阵微分的一大内容。因此，下面我们列出完整的定义。

自变量 / 因变量	矩阵 $\mathbf{F}$	向量 $\mathbf{f}$	标量 $f$
矩阵 $\mathbf{X}$	不讨论	不讨论	$\frac{\partial f}{\partial {\mathbf{X}}_{m\times n}}={\left[\frac{\partial f}{\partial x_{ij}}\right]}_{m\times n}$
向量 $\mathbf{x}$	不讨论	$\frac{\partial \mathbf{f}}{\partial \mathbf{x}}={\left[\begin{array}{ccccc}\frac{\partial f_1}{\partial x_1}& \frac{\partial f_2}{\partial x_1}& \frac{\partial f_3}{\partial x_1}& \cdots & \frac{\partial f_m}{\partial x_1}\\ \frac{\partial f_1}{\partial x_2}& \frac{\partial f_2}{\partial x_2}& \frac{\partial f_3}{\partial x_2}& \cdots & \frac{\partial f_m}{\partial x_2}\\ \frac{\partial f_1}{\partial x_3}& \frac{\partial f_2}{\partial x_3}& \frac{\partial f_3}{\partial x_3}& \cdots & \frac{\partial f_m}{\partial x_3}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ \frac{\partial f_1}{\partial x_n}& \frac{\partial f_2}{\partial x_n}& \frac{\partial f_3}{\partial x_n}& \cdots & \frac{\partial f_m}{\partial x_n}\end{array}\right]}_{n\times m}$	$\frac{\partial f}{\partial \mathbf{x}}={[\frac{\partial f}{\partial x_1},\frac{\partial f}{\partial x_2},\cdots ,\frac{\partial f}{\partial x_n}]}^T$
标量 $x$	$\frac{\partial {\mathbf{F}}_{m\times n}}{\partial x}={\left[\frac{\partial f_{ji}}{\partial x}\right]}_{n\times m}$	$\frac{\partial \mathbf{f}}{\partial x}=[\frac{\partial f_1}{\partial x},\frac{\partial f_2}{\partial x},\cdots ,\frac{\partial f_n}{\partial x}]$	平凡

So...列向量还是行向量？

在计算向量或矩阵的导数时，一个问题就是自变量、因变量和结果到底应该怎么排列呢？比如，分母应该是行向量还是列向量？结果呢？前文说过，这只是一个排列方式，似乎一个小小的转置并不重要。但我们最好还是仔细定义来澄清这一点。

一般而言，分为两种模式，即分子布局和分母布局。它们的选择是随意的，但在一次求导运算中，只能选择一种布局，不能杂糅。

上文的表格中，我们使用的就是分母布局。它的含义是，结果的维数必须要与分母的维数或分子的转置的维数相同。进一步说明：第一，我们只需要一个分子或分母的一个判据即可：也就是说，如果分母为标量，那只能看分子的转置，反之亦然。第二，当选择的判据是向量而结果是矩阵时，若是行向量就只用看矩阵的列数是否等于向量的维数，若是列向量就只看行数。

分子布局与分母布局刚刚相反，两者的差异在于一个转置。

但在实际应用中，我们往往会选择混合布局，即在一次求导运算中，我们可以选择不同的布局。这样做的好处是，可以减少转置的次数，提高计算效率。但是，这样可能会增加一些混乱，需要我们时刻注意自己选择的布局。

有了上面的说明，就可以利用微分学的知识和一点点代数的能力，推导出很多简明的结论。下面我们给出一些。

标量对向量

• $\frac{\partial {\mathbf{a}}^{\mathbf{T}}\mathbf{x}}{\partial \mathbf{x}}=\mathbf{a}$，其中 $\mathbf{a}$ 是一个常向量（这里“常”的意思是指不是关于 $\mathbf{x}$ 的函数，下同）；
• $\frac{\partial {\mathbf{x}}^{\mathbf{T}}\mathbf{x}}{\partial \mathbf{x}}=2\mathbf{x}$；
• $\frac{\partial {\mathbf{x}}^{\mathbf{T}}\mathbf{Ax}}{\partial \mathbf{x}}=\mathbf{A}\mathbf{x}+{\mathbf{A}}^T\mathbf{x}$，这是因为

$$[\frac{\partial {\mathbf{x}}^{\mathbf{T}}\mathbf{Ax}}{\partial \mathbf{x}}{]}_k=\frac{\partial \sum _i\sum _j{x}_i{x}_j{A}_{ij}}{\partial x_k}=\sum _{i=1}^n{x}_i(A_{ik}+A_{ki})$$

• $\frac{\partial {\mathbf{a}}^T\mathbf{x}{\mathbf{x}}^T\mathbf{b}}{\partial \mathbf{x}}=(\mathbf{a}{\mathbf{b}}^T+\mathbf{b}{\mathbf{a}}^T)\mathbf{x}$
• 若 $f,g$ 都是关于 $\mathbf{x}$ 在对应点可导的标量函数，则
  • $c_1\frac{\partial f}{\partial \mathbf{x}}+c_2\frac{\partial g}{\partial \mathbf{x}}=\frac{\partial (c_{1}f(\mathbf{x})+c_{2}g(\mathbf{x}))}{\partial \mathbf{x}}$；
  • $\frac{\partial f(\mathbf{x})\cdot g(\mathbf{x})}{\partial \mathbf{x}}=f(\mathbf{x})\frac{\partial g}{\partial \mathbf{x}}+g(\mathbf{x})\frac{\partial f}{\partial \mathbf{x}}$；
  • $\frac{\partial f(\mathbf{x})/g(\mathbf{x})}{\partial \mathbf{x}}=\frac{g(\mathbf{x})\frac{\partial f}{\partial \mathbf{x}}-f(\mathbf{x})\frac{\partial g}{\partial \mathbf{x}}}{g^2(\mathbf{x})}$；
  • $\frac{\partial f(g(\mathbf{x}))}{\partial \mathbf{x}}=\frac{\partial f}{\partial g}\frac{\partial g}{\partial \mathbf{x}}$；

这些结论通过学过的微分学知识和矩阵的性质可以推导出来。至于向量对标量的导数，相对而言就更加简单，这里就不再赘述。

向量对向量

先给出一些简单的结论：

• $\frac{\partial \mathbf{a}}{\partial \mathbf{x}}=\mathbf{0}$，其中 $\mathbf{a}$ 是一个常向量；
• $\frac{\partial \lambda \mathbf{x}}{\partial \mathbf{x}}=\lambda \mathbf{I}$，其中 $\lambda$ 是一个常标量，$\mathbf{I}$ 是单位矩阵；
• $\frac{\partial (\mathbf{u}+\mathbf{v})}{\partial \mathbf{x}}=\frac{\partial \mathbf{u}}{\partial \mathbf{x}}+\frac{\partial \mathbf{v}}{\partial \mathbf{x}}$，其中 $\mathbf{u},\mathbf{v}$ 是两个向量；
• $\frac{\partial \mathbf{g}\mathbf{(}\mathbf{u}\mathbf{)}}{\partial \mathbf{x}}=\frac{\partial \mathbf{g}\mathbf{(}\mathbf{u}\mathbf{)}}{\partial \mathbf{u}}\frac{\partial \mathbf{u}}{\partial \mathbf{x}}$，其中 $\mathbf{g}\mathbf{(}\mathbf{u}\mathbf{)}$ 是一个向量函数（输入向量、输出向量），$\mathbf{u}$ 是一个向量；

接下来是一些稍微复杂一点的结论：

• $\frac{\partial v\mathbf{u}}{\partial \mathbf{x}}=v\frac{\partial \mathbf{u}}{\partial \mathbf{x}}+\frac{\partial v}{\partial \mathbf{x}}{\mathbf{u}}^T$，其中 $v$ 是一个标量，$\mathbf{u}$ 是一个向量；(使用时一定要注意布局)
• $\frac{\partial \mathbf{Au}}{\partial \mathbf{x}}=\frac{\partial \mathbf{u}}{\partial \mathbf{x}}{\mathbf{A}}^T$，其中 $\mathbf{A}$ 是一个常矩阵，$\mathbf{u}$ 是一个向量；

其他常用结论

• $\frac{\partial \mathbf{AB}}{\partial x}=\frac{\partial \mathbf{A}}{\partial x}\mathbf{B}+\mathbf{A}\frac{\partial \mathbf{B}}{\partial x}$，其中 $\mathbf{A},\mathbf{B}$ 是两个常矩阵；由此，将 $A^{-1}$ 代替 $B$ 可以推出

$$\frac{\partial {\mathbf{A}}^{-1}}{\partial x}=-{\mathbf{A}}^{-1}\frac{\partial \mathbf{A}}{\partial x}{\mathbf{A}}^{-1}$$

• $\frac{\partial \mathrm{tr}(\mathbf{AB})}{\partial \mathbf{A}}={\mathbf{B}}^T$
• $\frac{\partial \mathrm{tr}({\mathbf{ABA}}^{\mathbf{T}})}{\partial \mathbf{A}}=A({\mathbf{B}}^T+\mathbf{B})$

协方差

在概率统计中，协方差用来衡量两个变量的相关程度。对于两个随机变量 $X$ 和 $Y$，它们的协方差定义为：

$$\begin{array}{rl}\mathrm{cov}(X,Y)& =E[(X-E(X))(Y-E(Y))]\\ & =\frac{1}{n}\sum _{i=1}^n(x_i-\overline{x})(y_i-\overline{y})\end{array}$$

其中，$E(X)$ 和 $E(Y)$ 分别是 $X$ 和 $Y$ 的期望。我们有如下的几个结论：

定理$1$ 如果 $X$ 和 $Y$ 相互独立，那么 $\mathrm{cov}(X,Y)=0$；但逆命题不成立（试着构造一个反例……）。

定理$2$ $\mathrm{cov}(X,Y)=E[XY]-E[X]\cdot E[Y]$

定理$3$ $\mathrm{cov}(X,X)=\mathrm{var}(X)$

定理$4$ $\mathrm{cov}(aX,bY)=ab\cdot \mathrm{cov}(X,Y)$

对于两列随机变量 $\overrightarrow{\mathbf{X}}=\{X_i{\}}_{i=1}^m,\overrightarrow{\mathbf{Y}}=\{Y_i{\}}_{i=1}^n$，我们有协方差矩阵：

$$\begin{array}{rl}\mathbf{cov}(\overrightarrow{\mathbf{X}},\overrightarrow{\mathbf{Y}})& =[\mathrm{cov}(X_i,Y_j){]}_{m\times n}\\ \\ & =\left[\begin{array}{cccc}\mathrm{cov}(X_1,Y_1)& \mathrm{cov}(X_1,Y_2)& \cdots & \mathrm{cov}(X_1,Y_n)\\ \mathrm{cov}(X_2,Y_1)& \mathrm{cov}(X_2,Y_2)& \cdots & \mathrm{cov}(X_2,Y_n)\\ ⋮& ⋮& \ddots & ⋮\\ \mathrm{cov}(X_m,Y_1)& \mathrm{cov}(X_m,Y_2)& \cdots & \mathrm{cov}(X_m,Y_n)\end{array}\right]\end{array}$$

可以看出，协方差矩阵是一个对称矩阵。对角线上的元素就是各个随机变量的方差。

例如，给定一个含有 $m$ 个属性、$n$ 个样本的数据集 $\mathbf{X}=\{{\mathbf{x}}_1,{\mathbf{x}}_2,\cdots ,{\mathbf{x}}_n\}$，其中 ${\mathbf{x}}_i$ 是一个 $m$ 维向量，代表了第 $i$ 个样本；而第 $j$ 个属性就用随机变量 ${\omega }_j$ 表示，第 $i$ 个样本的第 $j$ 个属性用 ${\omega }_{ji}$ 表示，所有这些属性的随机变量组成的向量用 $\overrightarrow{\omega }$ 表示，那么这一数据集的（也就是这些属性间的）协方差矩阵就是：

$$\begin{array}{rl}\mathrm{\Sigma }& =\mathbf{cov}(\overrightarrow{\omega },\overrightarrow{\omega })\\ & =[\mathrm{cov}({\omega }_i,{\omega }_j){]}_{m\times m}\\ & =\left[\begin{array}{cccc}\mathrm{cov}({\omega }_1,{\omega }_1)& \mathrm{cov}({\omega }_1,{\omega }_2)& \cdots & \mathrm{cov}({\omega }_1,{\omega }_m)\\ \mathrm{cov}({\omega }_2,{\omega }_1)& \mathrm{cov}({\omega }_2,{\omega }_2)& \cdots & \mathrm{cov}({\omega }_2,{\omega }_m)\\ ⋮& ⋮& \ddots & ⋮\\ \mathrm{cov}({\omega }_m,{\omega }_1)& \mathrm{cov}({\omega }_m,{\omega }_2)& \cdots & \mathrm{cov}({\omega }_m,{\omega }_m)\end{array}\right]\\ & =\frac{1}{n}\left[\begin{array}{cccc}\sum _{i=1}^n({\omega }_{1i}-{\overline{\omega }}_1)({\omega }_{1i}-{\overline{\omega }}_1)& \sum _{i=1}^n({\omega }_{1i}-{\overline{\omega }}_1)({\omega }_{2i}-{\overline{\omega }}_2)& \cdots & \sum _{i=1}^n({\omega }_{1i}-{\overline{\omega }}_1)({\omega }_{mi}-{\overline{\omega }}_m)\\ \sum _{i=1}^n({\omega }_{2i}-{\overline{\omega }}_2)({\omega }_{1i}-{\overline{\omega }}_1)& \sum _{i=1}^n({\omega }_{2i}-{\overline{\omega }}_2)({\omega }_{2i}-{\overline{\omega }}_2)& \cdots & \sum _{i=1}^n({\omega }_{2i}-{\overline{\omega }}_2)({\omega }_{mi}-{\overline{\omega }}_m)\\ ⋮& ⋮& \ddots & ⋮\\ \sum _{i=1}^n({\omega }_{mi}-{\overline{\omega }}_m)({\omega }_{1i}-{\overline{\omega }}_1)& \sum _{i=1}^n({\omega }_{mi}-{\overline{\omega }}_m)({\omega }_{2i}-{\overline{\omega }}_2)& \cdots & \sum _{i=1}^n({\omega }_{mi}-{\overline{\omega }}_m)({\omega }_{mi}-{\overline{\omega }}_m)\end{array}\right]\\ & =\frac{1}{n}\sum _{i=1}^n\left[\begin{array}{cccc}({\omega }_{1i}-{\overline{\omega }}_1)({\omega }_{1i}-{\overline{\omega }}_1)& ({\omega }_{1i}-{\overline{\omega }}_1)({\omega }_{2i}-{\overline{\omega }}_2)& \cdots & ({\omega }_{1i}-{\overline{\omega }}_1)({\omega }_{mi}-{\overline{\omega }}_m)\\ ({\omega }_{2i}-{\overline{\omega }}_2)({\omega }_{1i}-{\overline{\omega }}_1)& ({\omega }_{2i}-{\overline{\omega }}_2)({\omega }_{2i}-{\overline{\omega }}_2)& \cdots & ({\omega }_{2i}-{\overline{\omega }}_2)({\omega }_{mi}-{\overline{\omega }}_m)\\ ⋮& ⋮& \ddots & ⋮\\ ({\omega }_{mi}-{\overline{\omega }}_m)({\omega }_{1i}-{\overline{\omega }}_1)& ({\omega }_{mi}-{\overline{\omega }}_m)({\omega }_{2i}-{\overline{\omega }}_2)& \cdots & ({\omega }_{mi}-{\overline{\omega }}_m)({\omega }_{mi}-{\overline{\omega }}_m)\end{array}\right]\\ & =\frac{1}{n}\sum _{i=1}^n(\mathbf{x}-\overline{\mathbf{x}})(\mathbf{x}-\overline{\mathbf{x}}{)}^T\end{array}$$

条件概率与贝叶斯公式

对于在 $B$ 事件已发生条件下，$A$ 事件发生的概率，我们将它定义为条件概率 $P(A|B)$。

先验概率指在考虑某些已然确定的事实（观测数据）前估计的概率分布，而后验概率指将那些将观测数据纳入考虑范围时的概率。先验概率描述了随机变量本身的随机程度，而后验概率为基于试验和调查后得到的概率分布。

例如，$P(A)$ 是事件 $A$ 的先验概率，$P(A|B)$ 是在事件 $B$ 发生后 $A$ 的后验概率。贝叶斯公式就是描述这两者之间的关系：

$$P(A|B)=\frac{P(B|A)P(A)}{P(B)}$$

其中，$P(B|A)$ 是 $B$ 的后验概率，也被称作 $A$ 的似然，$P(A)$ 是 $A$ 的先验概率，$P(B)$ 是 $B$ 的先验概率，$P(B|A)/P(B)$ 称作可能性函数，也叫调整因子。因此，我们可以总结为：后验概率等于先验概率乘以可能性函数。

概率是已知参数的情况下观测到某一事件的可能性，而似然是在已知某一事件的情况下推测到某一参数的可能性。例如，对于一枚硬币上抛十次，如果假定硬币是均匀的（参数），那么我们可以求得到五次正面的概率；而如果我们已知抛十次硬币得到了五次正面，那么我们可以求得硬币是均匀的可能性，这就是似然。

已知有 $A$ 事件发生，$B$ 是在参数 $b$ 下发生的事件，我们定义似然函数 $L(b|A)$ 为

$$b\mapsto P(A|B=b)$$

需要注意的是，似然函数并不需要满足归一性，即 $\int L(b|A)\mathrm{d}b\ne 1$ 可以成立。一个似然函数乘上一个常数后，它仍是一个似然函数。因为，在似然分析中，我们通常关注的是参数的相对变化趋势。

例如，对于抛硬币的例子，已知事件 $A$ 是“抛十次硬币得到五次正面”，事件 $B$ 是“硬币集中在正面的分布是 $b$，即硬币抛出一次后，得到正面的概率是 $b$”。那么，我们可以定义似然函数为

$$\begin{array}{rl}L(b|A)& =P(A|B=b)\\ & =(\genfrac{}{}{0ex}{}{10}{5})b^5(1-b{)}^5\end{array}$$

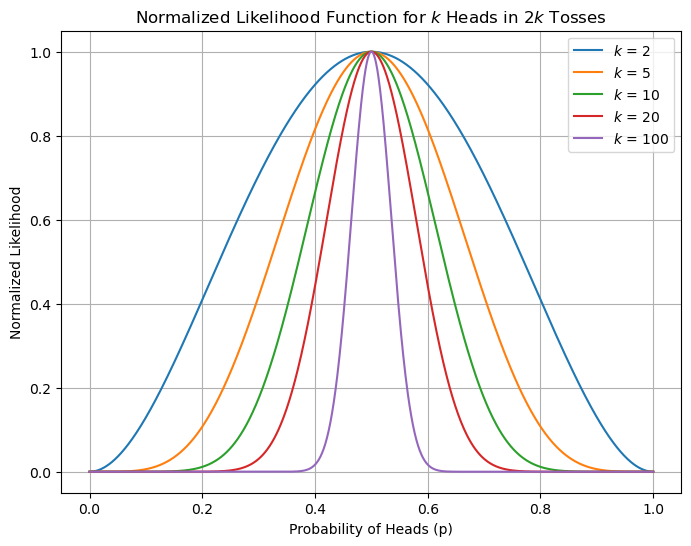
那么，我们可以通过似然函数来估计硬币的正面概率。下图绘制了这一似然函数的图像（$k=5$ 曲线）：

实现代码

# Try to run this code on your local machine!
import numpy as np
import matplotlib.pyplot as plt

p_values = np.linspace(0, 1, 1000)

def likelihood(p, k):
    return p**k * (1 - p)**k

k_values = [2,5,10,20,100]

plt.figure(figsize=(8, 6))
for k_value in k_values:
    likelihood_value = likelihood(p_values, k_value)
    normalized_likelihood_value = likelihood_value / np.max(likelihood_value)
    plt.plot(p_values, normalized_likelihood_value, label='$k$ = '+str(k_value))

plt.title('Normalized Likelihood Function for $k$ Heads in $2k$ Tosses')
plt.xlabel('Probability of Heads (p)')
plt.ylabel('Normalized Likelihood')
plt.grid(True)
plt.legend()
plt.show()

由上图我们也可以看出，随着上抛的次数增多，似然函数的峰值会越来越尖锐，这是因为随着抛硬币的次数增多，我们对硬币正面概率的估计会越来越准确。显然，当我们抛两次硬币得到一次正面时，和抛两百次硬币得到一百次正面时，我们对硬币均匀度的把握会有显著不同。这就是极大似然估计的核心思想。

在机器学习领域，通常我们会使用下面的记号：

• $p(y=i)$ 是类别 $i$ 的先验概率；
• $p(\mathbf{x})$ 是特征 $\mathbf{x}$ 的先验概率；
• $p(\mathbf{x}|y=i)$ 是类别 $i$ 的似然函数；
• $p(y=i|\mathbf{x})$ 是类别 $i$ 的后验概率；

距离度量函数

对于两个样本向量 $x_i,x_j\in {\mathbb{R}}^d$，我们希望计算它们之间的偏离程度。这就是距离度量函数。常见的各个距离度量函数的计算方法如下：

• 欧式距离$$d(x_i,x_j)=||x_i-x_j|{|}_2=\sqrt{(x_i-x_j{)}^T(x_i-x_j)}$$
• 余弦相似性（类似角度）$$s(x_i,x_j)=\frac{x_i^T{x}_j}{||x_i||\cdot ||x_j||}$$
• 曼哈顿距离 $d(x_i,x_j)=||x_i-x_j|{|}_1$
• 切比雪夫距离 $d(x_i,x_j)=||x_i-x_j|{|}_{\mathrm{\infty }}$
• 马氏距离$$d_M(x_i,x_j)=\sqrt{(x_i-x_j{)}^{T}M(x_i-x_j)}$$

范数

范数是一个函数，它将向量映射到非负值。对于一个向量 $\mathbf{x}\in {\mathbb{R}}^d$，它的 $p$ 范数定义为：

$$||\mathbf{x}|{|}_p={(\sum _{i=1}^d|x_i{|}^p)}^{1/p}$$

上文的曼哈顿距离、欧式距离和切比雪夫距离分别是 $1$ 范数、$2$ 范数和 $\mathrm{\infty }$ 范数的特例。

马氏距离的计算

马氏距离的 $M$ 是各维度的协方差矩阵的逆，它是一个 $d\times d$ 的矩阵，其中 $d$ 是向量的维数。

例如，对于三个样本向量 ${\mathbf{x}}_1,{\mathbf{x}}_2,{\mathbf{x}}_3\in {\mathbb{R}}^2，{\mathbf{x}}_1=[1,2{]}^T,{\mathbf{x}}_2=[2,3{]}^T,{\mathbf{x}}_3=[3,4{]}^T$，我们可以按照如下方法计算它们之间的马氏距离：

• 计算协方差矩阵 $\mathrm{\Sigma }$：
  • 确定各维度向量 $\mathbf{m}=[1,2,3{]}^T$，$\mathbf{n}=[2,3,4{]}^T$；
  • 计算协方差矩阵 $\mathrm{\Sigma }=\mathbf{cov}(\mathbf{m},\mathbf{n})$；
• 计算协方差矩阵的逆 $M={\mathrm{\Sigma }}^{-1}$；
• 计算马氏距离 $d_M({\mathbf{x}}_i,{\mathbf{x}}_j)=\sqrt{({\mathbf{x}}_i-{\mathbf{x}}_j{)}^{T}M({\mathbf{x}}_i-{\mathbf{x}}_j)}$。

马氏距离的优点是，相对欧式距离更加准确，因为它考虑了各维度之间的相关性并进行了归一化。

高斯分布

高斯分布是一种连续概率分布，也称为正态分布。正态分布是在统计中以及众多统计测试中最广泛应用的一类分布。它的概率密度函数为：

$$f(x|\mu ,{\sigma }^2)=\frac{1}{\sqrt{2\pi }\sigma }{e}^{-\frac{(x-\mu {)}^2}{2{\sigma }^2}}$$

其中，$\mu$ 是均值，${\sigma }^2$ 是方差。正态分布的均值和方差分别决定了分布的位置和形状。正态分布的概率密度函数是一个钟形曲线，它的均值是对称轴，方差决定了曲线的“胖瘦”。

对于 $d$ 维随机变量 $\mathbf{x}\in {\mathbb{R}}^d$ 服从多元高斯分布，其概率密度函数为：

$$f(\mathbf{x}|\mu ,\mathbf{\Sigma })=\frac{1}{(2\pi {)}^{d/2}|\mathbf{\Sigma }{|}^{1/2}}\exp \left(-\frac{1}{2}(\mathbf{x}-\mu {)}^T{\mathbf{\Sigma }}^{-1}(\mathbf{x}-\mu )\right)$$

其中，$\mu$ 是均值向量，$\mathbf{\Sigma }$ 是协方差矩阵。

信息熵