Regular Expressions
Regular expressions describe languages based on algebra operations. The language defined by regular expression
Regular Expression Definition (Bases)
A regular expression is defined as follows:
- Basis1: If
- Basis2:
- Basis3:
Regular Expression Operators (Inductions)
The regular expression operators are defined as follows:
- Induction 1 (Union): If
- Induction 2 (Concatenation): If R1 and R2 are regular expressions, then
- Induction 3 (Kleene Star): If
Precedence of Operators
The precedence of operators is as follows:
- Kleene Star has the highest precedence.
- Concatenation has the second highest precedence. The concatenation operator is implicit, so it is not necessary to write it.
- Union has the lowest precedence.
Regular Expression Examples
- Example 1:
- Example 2:
Equivalence of Regular Expressions and Finite Automata
Regular expressions and finite automata are equivalent. A regular expression can be easily converted to a NFA by using Thompson's construction method. For any regular expression
Basic Rules
- If the regular expression is a symbol

R is only a symbol 'a'
- If the regular expression

R is epsilon
- If the regular expression is
- If the regular expression is a symbol
Inductive Rules
- If the regular expression is
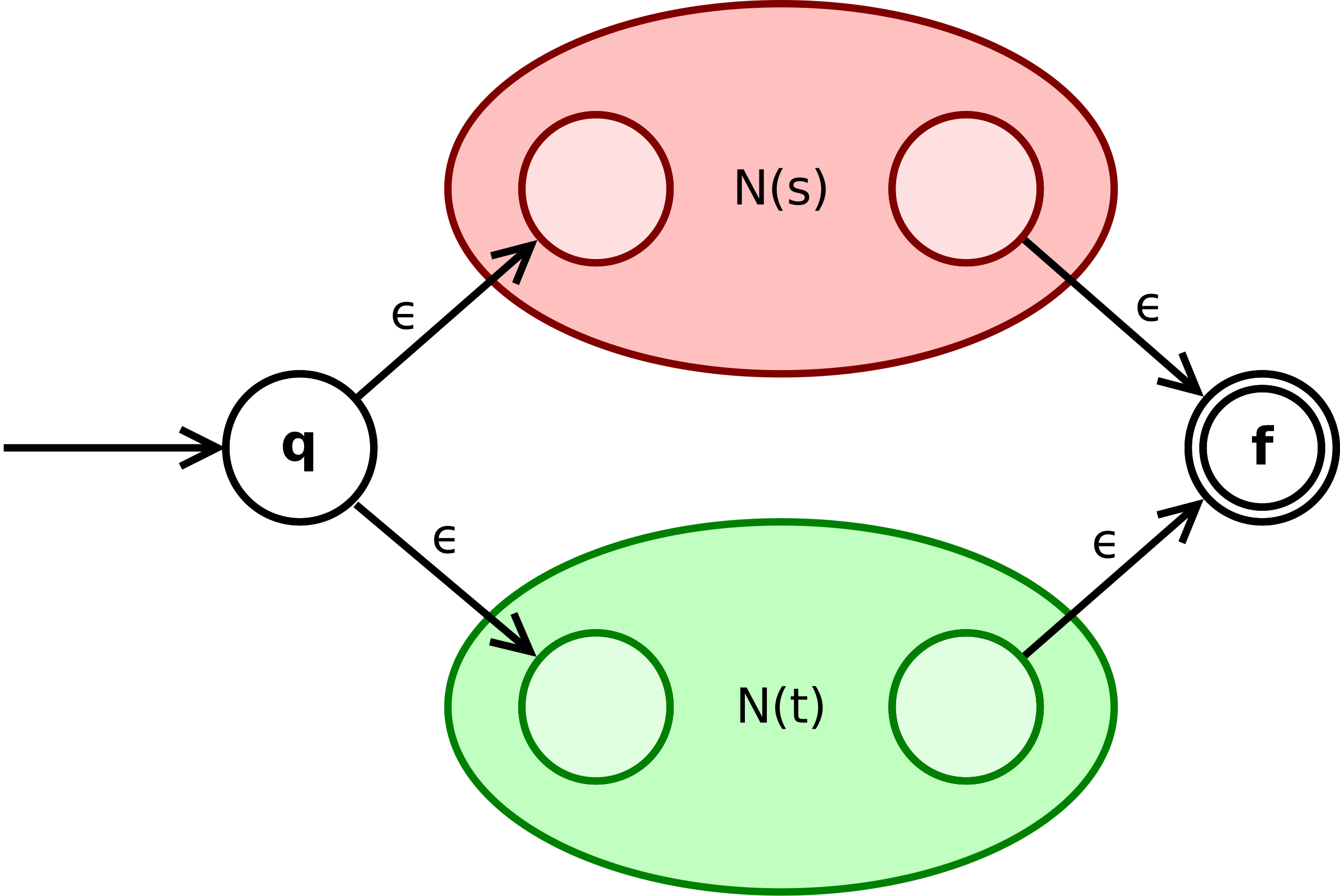
R is s + t
- If the regular expression is
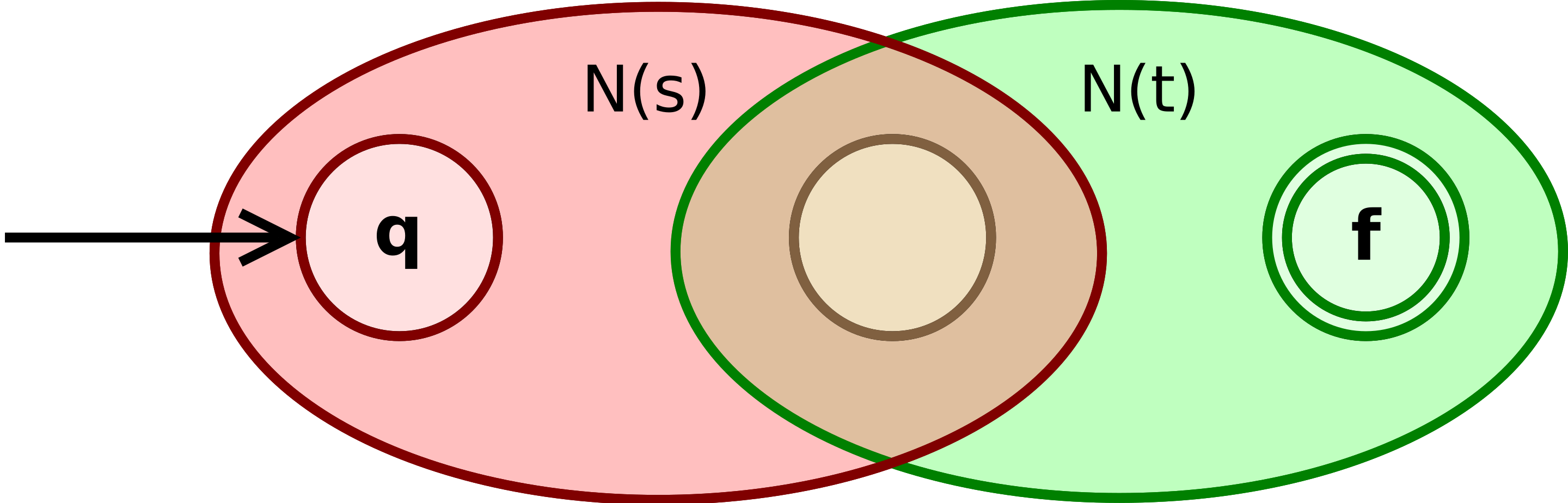
R is s.t
- If the regular expression is
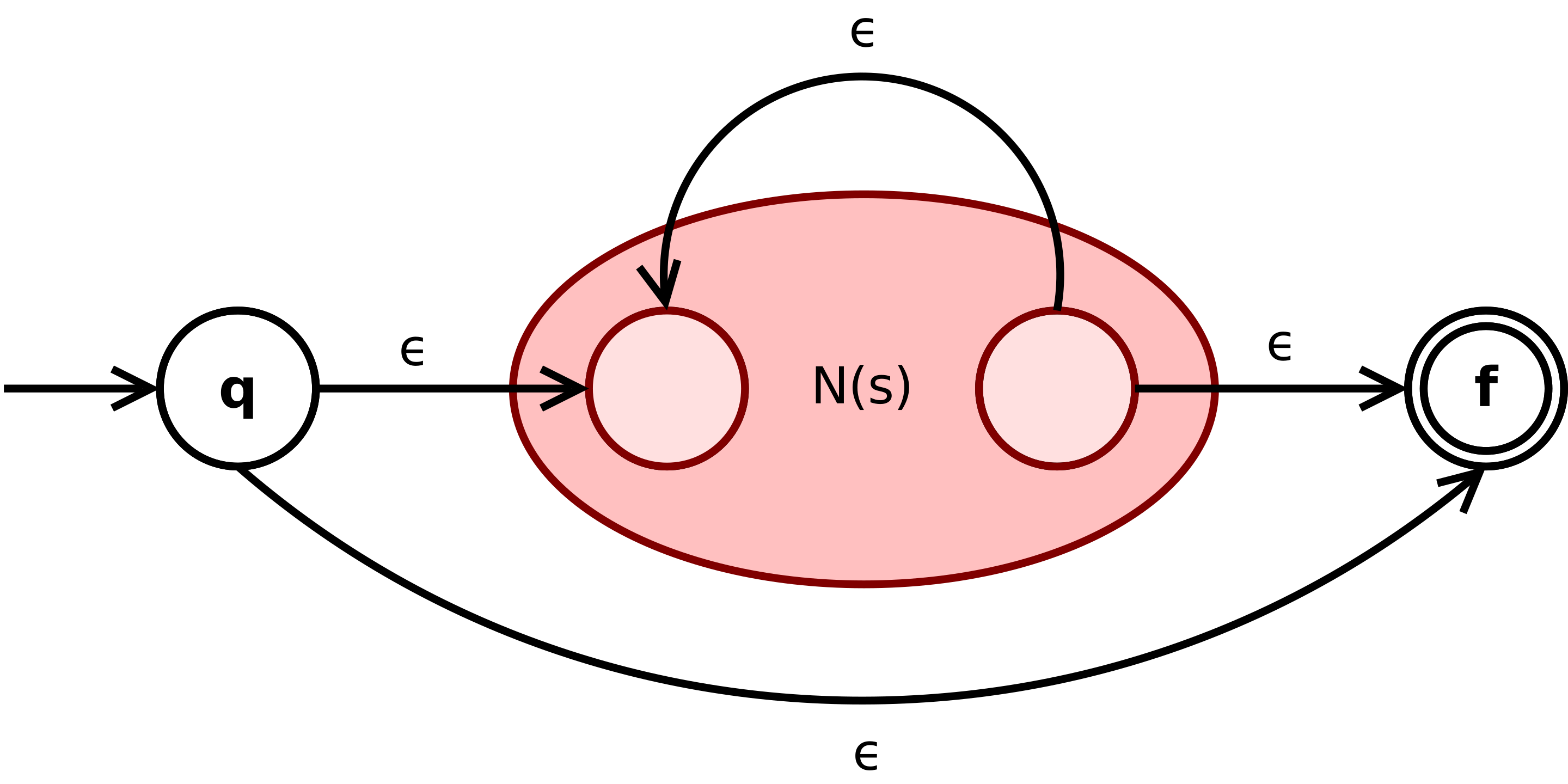
R is s*
- If the regular expression is
DFA to
First, we need to define the concept of
The idea of the algorithm is to find the corresponding regular expression for the
Let
- Basis: For
- Induction: For
- The
- The
- The
- The
Finally, the regular expression for the language of the DFA is
Summary
Each of the three types of automata (DFA, NFA,
