Properties of Context-Free Languages

Emptiness Problem

We learned to eliminate useless symbols and productions from a CFG. We can use this to solve the emptiness problem for CFGs. Apparently, if the start symbol is useless, then the language generated by the CFG is empty. Otherwise, the language is nonempty.

Membership Problem

We want to determine whether a given string $\omega$ is in the language generated by a CFG. A fast approach is the CYK algorithm. It is a good example of dynamic programming, with the time complexity of $O(n^3)$, where $n$ is the length $\omega$.

CYK Algorithm We denote $w=a_1{a}_2\cdots a_n$. Let $A$ be the $n\times n$ matrix and $A_{ij}$ be the set of non-terminals that generate the substring $a_i{a}_{i+1}\cdots a_j$. The production set is $P$. Then we have the following algorithm:

• Basis: $X_{ii}=\{A\mid A\to a_i\in P\}$
• Induction: $X_{ij}=\{A\mid A\to BC\in P,B\in X_{ik},C\in X_{k+1,j}\}$

Finally, we check whether the start symbol is in $X_{1n}$.

The CYK algorithm can be implemented in a three level nested loop. We show a pseudocode below:

for i = 1 to n
    X[i][i] = {A | A -> a[i] in P}
    
for l = 2 to n
    for i = 1 to n-l+1
        j = i + l - 1
        for k = i to j-1
            for each production A -> BC in P
                if B in X[i][k] and C in X[k+1][j]
                    add A to X[i][j]
if S in X[1][n]
    return "yes"
else
    return "no"

Infiniteness Problem

The idea is essentially the same as the regular language. We can use the pumping lemma for CFLs to prove that a language is infinite. The proof is similar to the regular language case.

The conclusion is that if a string in the language of the length between $n$ and $2n-1$, then the language is infinite, otherwise, it is finite.

Closure Properties

CFLs are closed under union, concatenation, and Kleene star. Also, they are closed under homomorphism, inverse homomorphism, and intersection with regular languages. But not under intersection, difference, and complementation.

However, A CFL is closed under intersection with a regular language. The proof is simple. We can imagine a DFA and PDA running in parallel. But from the outside, the multiple machines can be regarded as only a single PDA.

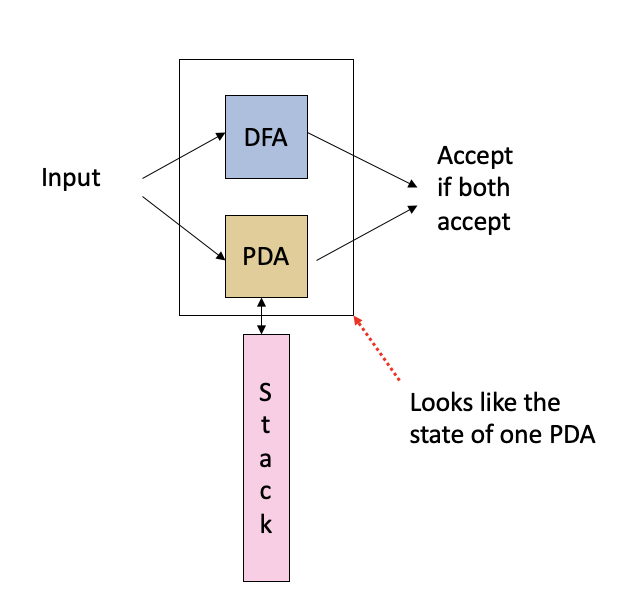
Two in Parallel