Closure Properties of Regular Languages

Closure Properties

A closure property of a class of languages says that given languages in the class, the operation on the languages results in a language that is also in the class. For example, the class of regular languages is closed under union, concatenation, and Kleene star operations.

Closure of Regular Languages

Closure under Union, Concatenation, and Kleene Star

If $L_1$ and $L_2$ are regular languages, so is $L_1\cup L_2$.

Proof Let $R_1$ and $R_2$ be regular expressions for $L_1$ and $L_2$, respectively. Then, $R_1+R_2$ is a regular expression for $L_1\cup L_2$. Therefore, $L_1\cup L_2$ is a regular language. (Regular languages are equivalent to languages that can be generated by regular expressions.)

We can also prove closure under concatenation and Kleene star operations in a similar way.

Closure under Intersection, Difference, and Complement

If $L_1$ and $L_2$ are regular languages, so is $L_1\cap L_2$.

Proof Let $M_1$ and $M_2$ be DFAs for $L_1$ and $L_2$, respectively. Then, we can construct a DFA $M$ for $L_1\cap L_2$ by taking the Cartesian product of the states of $M_1$ and $M_2$. We make the final state of $M$ the pairs consisting of final states of both $M_1$ and $M_2$.

We can also prove closure under difference and complement operation in a similar way.

Closure under Reversal

If $L$ is a regular language, so is $L^R$.

Proof Let $R$ be a regular expression for $L$. We can define the reverse of $R$ as follows:

• Basis: If $E$ is a symbol, $\epsilon$, or $\mathrm{\varnothing }$, then $E^R=E$.
• Induction:
  • If $E$ is $F+G$, then $E^R=F^R+G^R$.
  • If $E$ is $FG$, then $E^R=G^R{F}^R$.
  • If $E$ is $F^{\ast }$, then $E^R=(F^R{)}^{\ast }$.

Therefore, $R^R$ is a regular expression for $L^R$. Hence, $L^R$ is a regular language.

Closure under Homomorphism

A homomorphism on an alphabet $\mathrm{\Sigma }$ is a function $h:\mathrm{\Sigma }\to {\mathrm{\Delta }}^{\ast }$, where $\mathrm{\Delta }$ is another alphabet. A homomorphism $h$ can be extended to strings in ${\mathrm{\Sigma }}^{\ast }$ as follows: $h(w)=h(w_1)h(w_2)\cdots h(w_n)$, where $w=w_1{w}_2\cdots w_n$. In this situlation, $h$ is a homomorphism from ${\mathrm{\Sigma }}^{\ast }$ to ${\mathrm{\Delta }}^{\ast }$.

If $L$ is a regular language, so is $h(L)$. $h(L)=\{h(w)\mid w\in L\}$.

Proof Let $R$ be a regular expression for $L$. We can define a regular expression $S$ for $h(L)$ as follows:

• Basis: If $E$ is a symbol, $\epsilon$, or $\mathrm{\varnothing }$, then $S=h(E)$.
• Induction:
  • If $E$ is $F+G$, then $S=h(F)+h(G)$.
  • If $E$ is $FG$, then $S=h(F)h(G)$.
  • If $E$ is $F^{\ast }$, then $S=(h(F){)}^{\ast }$.

Therefore, $S$ is a regular expression for $h(L)$. Hence, $h(L)$ is a regular language.

Closure under Inverse Homomorphism

Give homomorphism $h:{\mathrm{\Sigma }}^{\ast }\to {\mathrm{\Delta }}^{\ast }$ and $L\subseteq {\mathrm{\Delta }}^{\ast }$, the inverse homomorphism $h^{-1}:{\mathrm{\Delta }}^{\ast }\to {\mathrm{\Sigma }}^{\ast }$ is defined as follows: $h^{-1}(a)=\{w\in {\mathrm{\Sigma }}^{\ast }\mid h(w)\in L\}$. In other words, $h^{-1}(L)$ consists of strings whose homomorphic images are in $L$.

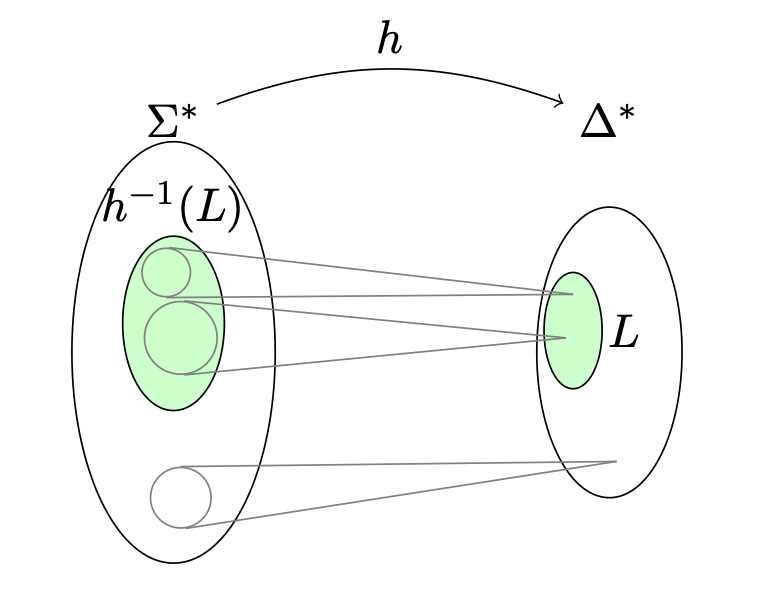
Inverse Homomorphism

For example, let $\mathrm{\Sigma }=\{a,b\}$ and $\mathrm{\Delta }=\{0,1\}$. Let $h(a)=01$, $h(b)=10$, and $L=(00\cup 1{)}^{\ast }$. Then, $h^{-1}(1001)=\{ba\}$, $h^{-1}(L)=(ba{)}^{\ast }$.

If $L$ is a regular language, so is $h^{-1}(L)$.