支持向量机

感知机

我们先来考虑一个感知机的问题。如何寻找一个能将数据集分成两类的超平面？对于线性可分的数据集，可能有很多很多选择。那么，我们应该如何选择一个“最好的”、泛化能力最强的超平面呢？我们可能会想到前文的线性判别分析，但这一算法不能将数据集完全分开。直觉告诉我们，我们应该选择一个在两类样本正中间的超平面。这个超平面距离两类样本的最近点的距离最远。的确，这一算法在实际的模型中表现较好，并且如果利用核函数，该算法还适用于线性不可分的情况。有了这一直观的感受的基础，我们就给出下面的定义：

一个点对应的间隔是指其到分界超平面的垂直距离。SVM 最大化所有训练样本的最小间隔。具有最小间隔的点叫做支持向量。

对于一个分类超平面 $w^{T}x+b=0$，其法向量为 $w$，那么点 $x$ 到超平面的距离为：

$$\frac{|w^{T}x+b|}{\parallel w\parallel }$$

推导过程

下面的推导，可以通过平面情况画图辅助理解。

假设超平面 $f(\mathbf{x})={\mathbf{w}}^T\mathbf{x}+b=0$，其中 $w$ 是超平面的法向量，$b$ 是超平面的截距。令 $\mathbf{x}$ 的投影点为 ${\mathbf{x}}_{\perp }$，则 $\mathbf{x}-{\mathbf{x}}_{\perp }$ 即为距离向量，设其大小为 $r$（可正可负），方向为 $\frac{\mathbf{w}}{\parallel \mathbf{w}\parallel }$，则有：

$$\begin{array}{r}\mathbf{x}-{\mathbf{x}}_{\perp }=r\frac{\mathbf{w}}{\parallel \mathbf{w}\parallel }\\ \mathbf{x}={\mathbf{x}}_{\perp }+r\frac{\mathbf{w}}{\parallel \mathbf{w}\parallel }\\ {\mathbf{w}}^T\mathbf{x}+b={\mathbf{w}}^T{\mathbf{x}}_{\perp }+b+r\frac{{\mathbf{w}}^T\mathbf{w}}{\parallel \mathbf{w}\parallel }\\ f(\mathbf{x})=f({\mathbf{x}}_{\perp })+r\parallel \mathbf{w}\parallel \end{array}$$

由于 $f({\mathbf{x}}_{\perp })=0$，所以有：

$$r=\frac{f(\mathbf{x})}{\parallel \mathbf{w}\parallel }=\frac{{\mathbf{w}}^T\mathbf{x}+b}{\parallel \mathbf{w}\parallel }$$

为了方便，我们规定距离为正，那么 $|r|=\frac{|{\mathbf{w}}^T\mathbf{x}+b|}{\parallel \mathbf{w}\parallel }$。$◻$

对于这一公式，是不是和高中的点到直线的距离公式很像呢？例如，给定直线 $Ax+By+C=0$，点 $(x_0,y_0)$ 到直线的距离为

$$\frac{|A{x}_0+B{y}_0+C|}{\sqrt{A^2+B^2}}$$

这一公式的推导也是类似的。

线性支持向量机

分类与评价

• 怎样分类？当 $f(\mathbf{x})>0$ 时 $\mathbf{x}$ 属于正类，当 $f(\mathbf{x})<0$ 时 $\mathbf{x}$ 属于负类。
• 对于任何一个样例，我们可以通过将真实标签乘上预测标签，得到一个值。如果该值为正，则说明预测正确，否则预测错误。假设我们的标签满足 $y\in \{-1,1\}$，那么针对一个预测及其准确的模型，它的预测结果应该满足 $y_{i}f(x_i)=|f(x_i)|$。

SVM 的形式化描述

SVM 解决的问题就是求一个优化问题：

$$\begin{array}{r}{\mathrm{argmax}}_{w,b}\left[\underset{i}{min}\left(\frac{|{\mathbf{w}}^T{\mathbf{x}}_i+b|}{||\mathbf{w}||}\right)\right]\\ ={\mathrm{argmax}}_{w,b}\left[\underset{i}{min}\left(\frac{y_i({\mathbf{w}}^T{\mathbf{x}}_i+b)}{||\mathbf{w}||}\right)\right]\end{array}$$

目前为止，由于 $\mathbf{w}$ 没有限制，所以这一问题比较难优化。但我们发现，${\mathbf{w}}^{T}x+b$ 的大小对分类的结果没有影响，因此，我们只需要关心 $(\mathbf{w},b)$ 的方向即可。我们可以把 $\mathbf{w}$ 的长度限制为 1，这样我们就可以得到一个优化问题：

$$\begin{array}{r}{\mathrm{argmax}}_{w,b}\left[\underset{i}{min}(y_{i}f({\mathbf{x}}_i))\right]\\ \text{s.t. }{y}_{i}f({\mathbf{x}}_i)>0,1\le i\le n\\ {\mathbf{w}}^T\mathbf{w}=1\end{array}$$

假设某个最优解为 $({\mathbf{w}}^{\ast },b^{\ast })$，那么我们令一个常数 $c=\underset{1\le i\le n}{min}{y}_i(({\mathbf{w}}^{\ast }{)}^T\mathbf{x}+b^{\ast })$，显然，$\frac{1}{c}({\mathbf{w}}^{\ast },b^{\ast })$ 也是一个最优解。我们代入后发现

$$\underset{1\le i\le n}{min}{y}_i(({\frac{1}{c}\mathbf{w}}^{\ast }{)}^T\mathbf{x}+\frac{b^{\ast }}{c})=1>0$$

因此，我们可以限制 $\underset{i}{min}{y}_i({\mathbf{w}}^T\mathbf{x}+b)=1$，这样我们就可以得到一个更简单的优化问题，并且不改变最优解。如下方示意图，这一限制在图中表现为两条虚线（高维空间则为超平面）：

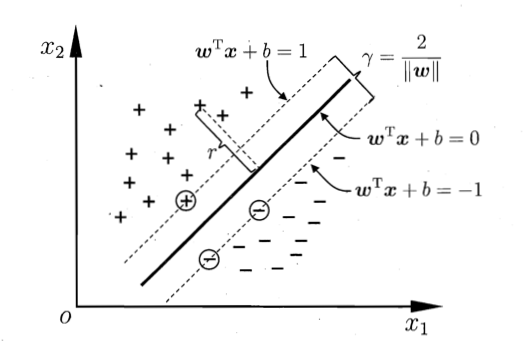
支持向量与间隔的示意图

下面问题就变为在限制 $\underset{i}{min}{y}_i({\mathbf{w}}^T\mathbf{x}+b)=1$ 的情况下，最大化间隔，即最大化 $\frac{1}{||\mathbf{w}||}$。形式化表述又可转为

$$\begin{array}{rl}{\mathrm{argmin}}_{w,b}& \frac{1}{2}||\mathbf{w}|{|}^2\\ \text{s.t. }{y}_i({\mathbf{w}}^T\mathbf{x}+b)\ge 1,& 1\le i\le n\end{array}$$

下面，我们使用拉格朗日乘子法来求解。令拉格朗日乘子为 ${\alpha }_i\ge 0$，则拉格朗日函数为

$$L(\mathbf{w},b,\alpha )=\frac{1}{2}||\mathbf{w}|{|}^2-\sum _{i=1}^n{\alpha }_i(y_i({\mathbf{w}}^T\mathbf{x}+b)-1)$$

为什么拉格朗日乘子非负？KKT 条件是什么？

常见的拉格朗日乘子法是在约束为等式 $g(\mathbf{x})=0$ 的情况下，求解 $E(\mathbf{x})$ 的最大值或最小值。在约束为等式的这种情况下，我们不对拉格朗日乘子 $\lambda$ 的正负进行限制，只需满足 $\mathrm{\nabla }E=\lambda \mathrm{\nabla }g$ 即可。

下面我们考虑约束为不等式的情况。例如求解最小化问题

$${\mathrm{argmin}}_{\mathbf{x}}E(\mathbf{x})\text{s.t. }g(\mathbf{x})\ge 0$$

我们可以通过引入拉格朗日乘子 $\lambda$，得到拉格朗日函数

$$L(\mathbf{x},\lambda )=E(\mathbf{x})-\lambda g(\mathbf{x})$$

我们尝试把它转换为求解函数 $L$ 的最小值的问题。对其求导可得

$$\begin{array}{rl}\mathrm{\nabla }{L}_{\mathbf{x}}& =\mathrm{\nabla }E-\lambda \mathrm{\nabla }g\\ \mathrm{\nabla }{L}_{\lambda }& =g(\mathbf{x})\end{array}$$

但显然，我们需要对其施加更多的约束。首先，我们要将 $g(x)\ge 0$ 的限制继承下来。其次我们发现，如果最小值点在 $g(x)<0$ 的范围内，则有 $\mathrm{\nabla }E=0$，此时 $\lambda$ 取 $0$ 即可；如果最小值点刚好在 $g(x)=0$ 这一边界上，则必须有 $\mathrm{\nabla }E$ 和 $\mathrm{\nabla }g$ 同向（如果反向，我们沿着 $\mathrm{\nabla }E$ 方向移动，可以使得 $E$ 减小并使得 $g$ 不变大，这样 $E$ 就不是最小值了）。所以我们必须规定 $\lambda \ge 0$。经过这一讨论，我们还发现，当取得最小值时，我们有 $\lambda g=0$。

综合上述讨论，我们得到了 KKT 条件：

$$\begin{array}{rl}g(\mathbf{x})& \ge 0\\ \lambda & \ge 0\\ \lambda g(\mathbf{x})& =0\end{array}$$

下图是另一种，$E$ 需要最大化的情况，可以进行对比思考。

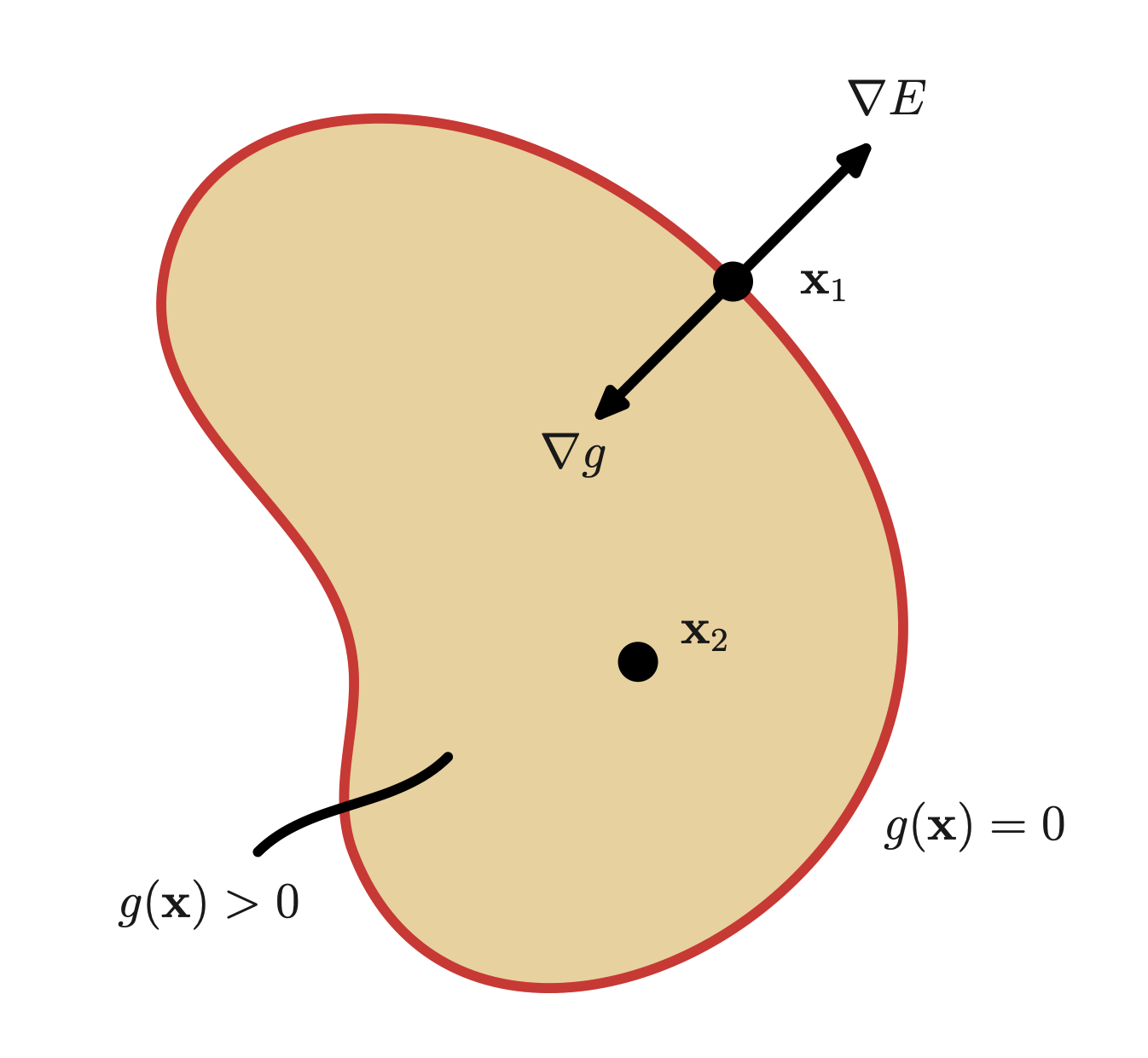
最大化 E

当最优时，有

$$\begin{array}{rl}\frac{\partial L}{\partial \mathbf{w}}& =\mathbf{w}-\sum _{i=1}^n{\alpha }_i{y}_i{\mathbf{x}}_i=0\\ \frac{\partial L}{\partial b}& =-\sum _{i=1}^n{\alpha }_i{y}_i=0\end{array}$$

将结果代回拉格朗日函数，我们可以得到新的拉格朗日函数 $L^{\ast }(\alpha )$

$$L^{\ast }(\alpha )=\sum _{i=1}^n{\alpha }_i-\frac{1}{2}\sum _{i=1}^n\sum _{j=1}^n{\alpha }_i{\alpha }_j{y}_i{y}_j{\mathbf{x}}_i^T{\mathbf{x}}_j$$

将我们的结果总结一下，利用 $\text{Karush-Kuhn-Tucker}$（KKT）条件，我们就得到了：

$$\begin{array}{r}\mathbf{w}=\sum _{i=1}^n{\alpha }_i{y}_i{\mathbf{x}}_i\\ \sum _{i=1}^n{\alpha }_i{y}_i=0\\ {\alpha }_i\ge 0\\ {\alpha }_i(y_i({\mathbf{w}}^T\mathbf{x}+b)-1)=0\\ y_i({\mathbf{w}}^T\mathbf{x}+b)-1\ge 0\end{array}$$

其中 ${\alpha }_i(y_i({\mathbf{w}}^T\mathbf{x}+b)-1)=0$ 称为互补松弛性质。一般来说，KKT 条件不是充分必要的。

SVM 的对偶形式

在原来的空间中，我们研究的变量是 ${\mathbf{x}}_i$，这称为 SVM 的原始形式。而当我们经过拉格朗日乘子法后，我们研究的变量变为 ${\alpha }_i$，这称为 SVM 的对偶形式。我们可以通过求解对偶问题来得到原始问题的解。

假设我们在对偶空间中，我们已经求得了最优的 ${\alpha }^{\ast }$。对于 ${\mathbf{w}}^{\ast }$，我们可以通过

$${\mathbf{w}}^{\ast }=\sum _{i=1}^n{\alpha }_i^{\ast }{y}_i{\mathbf{x}}_i$$

求得。对于 $b^{\ast }$，我们可以通过互补松弛性质，如果 ${\alpha }_i^{\ast }>0$，那么

$$y_i({\mathbf{w}}^T{\mathbf{x}}_i+b)=1$$

由此，对于某一个特定的 $b_i^{\ast }$，我们有

$$b_i^{\ast }=y_i-({\mathbf{w}}^{\ast }{)}^T{\mathbf{x}}_i$$

而对于所有样本，我们取其平均值即可

$$b^{\ast }=\frac{1}{n}\sum _{{\alpha }_i^{\ast }>0}(y_i-({\mathbf{w}}^{\ast }{)}^T{\mathbf{x}}_i)$$

Soft Margin 软间隔

对于原先的强约束 $y_i({\mathbf{w}}^T\mathbf{x}+b)\ge 1$，我们可以引入一个松弛变量 ${\xi }_i\ge 0$，使得约束变为 $y_i({\mathbf{w}}^T\mathbf{x}+b)\ge 1-{\xi }_i$。这样，我们的模型就会对于一些线性难以区分的样本有一定的容忍度，对噪声数据的适应性也会增加。

但是，犯错误是会受到惩罚的。我们可以通过引入一个正则化 $C$，使得我们的优化问题变为

$$\begin{array}{rl}{\mathrm{argmin}}_{w,b,\xi }& \frac{1}{2}||\mathbf{w}|{|}^2+C\sum _{i=1}^n{\xi }_i\\ \text{s.t. }{y}_i({\mathbf{w}}^T\mathbf{x}+b)\ge 1-{\xi }_i,& 1\le i\le n\\ {\xi }_i\ge 0,& 1\le i\le n\end{array}$$

通过调整 $C$ 的大小，我们可以控制模型对于噪声数据的容忍度，或说对错误的容忍度。

在对偶空间中，我们的拉格朗日函数其实没有改变，只是对于 ${\alpha }_i$ 的约束条件变为了 $0\le {\alpha }_i\le C$。

非线性支持向量机

当数据集是线性可分的时候，线性支持向量机的表现是非常好的。但是，当数据集是线性不可分的时候，我们就需要引入核函数来将数据映射到高维空间中，使得数据集变得线性可分。显然，当原始空间是有限维时，那么一定存在一个高维特征空间使样本可分。这就是一种非线性支持向量机的基本思想。

核函数

我们可以看下面一个例子： 假设 $\mathbf{x}=(x_1,x_2),\mathbf{y}=(y_1,y_2)$，我们可以定义一个二次多项式核函数 $K(\mathbf{x},\mathbf{y})=({\mathbf{x}}^T\mathbf{y}+1{)}^2$。展开并分解可发现：

$$\begin{array}{rl}K(\mathbf{x},\mathbf{y})& =({\mathbf{x}}^T\mathbf{y}+1{)}^2\\ & =(x_1{y}_1+x_2{y}_2+1{)}^2\\ & =x_1^2{y}_1^2+x_2^2{y}_2^2+1+2x_1{y}_1+2x_2{y}_2+2x_1{x}_2{y}_1{y}_2\\ & ={\left(\begin{array}{c}{x}_1^2\\ x_2^2\\ 1\\ \sqrt{2}{x}_1\\ \sqrt{2}{x}_2\\ \sqrt{2}{x}_1{x}_2\end{array}\right)}^T\left(\begin{array}{c}{y}_1^2\\ y_2^2\\ 1\\ \sqrt{2}{y}_1\\ \sqrt{2}{y}_2\\ \sqrt{2}{y}_1{y}_2\end{array}\right)\end{array}$$

如果定义 $\varphi (\mathbf{x})=\left(\begin{array}{c}{x}_1^2\\ x_2^2\\ 1\\ \sqrt{2}{x}_1\\ \sqrt{2}{x}_2\\ \sqrt{2}{x}_1{x}_2\end{array}\right)$，那么我们可以得到 $K(\mathbf{x},\mathbf{y})=\varphi (\mathbf{x}{)}^T\varphi (\mathbf{y})$。这样的 $K$ 称为核函数，而 $\varphi$ 称为特征映射。原来的 $\mathbf{x}$ 空间称为原始空间，而 $\varphi (\mathbf{x})$ 空间称为特征空间。

核支持向量机

我们利用核函数，可以将原来的优化问题转化为：

• 对偶形式：

$${\text{argmax}}_a\sum _{i=1}^n{\alpha }_i-\frac{1}{2}\sum _{i=1}^n\sum _{j=1}^n{\alpha }_i{\alpha }_j{y}_i{y}_{j}K({\mathbf{x}}_i,{\mathbf{x}}_j)$$

• 分类边界：$\mathbf{w}=\sum _{i=1}^n{\alpha }_i{y}_i\varphi ({\mathbf{x}}_i)$

• 预测：

$${\mathbf{w}}^T\varphi (\mathbf{x})=\varphi (\mathbf{x}{)}^T[\sum _{i=1}^n{\alpha }_i{y}_i\varphi ({\mathbf{x}}_i)]=\sum _{i=1}^n{\alpha }_i{y}_{i}K(\mathbf{x},{\mathbf{x}}_i)$$

这样，我们就可以通过核函数将数据映射到高维空间中，使得数据集在新的空间中变得线性可分。

下面，我们给出判断特征映射存在的一个充要条件：

$\text{Mercer}$ 条件

对于任何满足 $\int g^2(\mathbf{u})\mathrm{d}\mathbf{u}<\mathrm{\infty }$ 的非零函数（平方可积函数），对称函数 $K$ 满足:

$$\iint K(\mathbf{x},\mathbf{u})g(\mathbf{x})g(\mathbf{u})\mathrm{d}\mathbf{x}\mathrm{d}\mathbf{u}\ge 0$$

则称 $K$ 满足 $\text{Mercer}$ 条件。

一种等价形式是：对于任何一个样本集合 $\{{\mathbf{x}}_1,{\mathbf{x}}_2,\cdots ,{\mathbf{x}}_n\}$，其对应的核矩阵 $\mathbf{K}=K(x_i,x_j)$ 都满足 $\mathbf{K}$ 是半正定的，那么 $K$ 满足 $\text{Mercer}$ 条件。

常见核函数

• 线性核函数：$K(\mathbf{x},\mathbf{y})={\mathbf{x}}^T\mathbf{y}$
• 多项式核函数：$K(\mathbf{x},\mathbf{y})=(\gamma {\mathbf{x}}^T\mathbf{y}+c{)}^d$
• 高斯核函数：$K(\mathbf{x},\mathbf{y})=\exp (-\gamma ||\mathbf{x}-\mathbf{y}|{|}^2)$

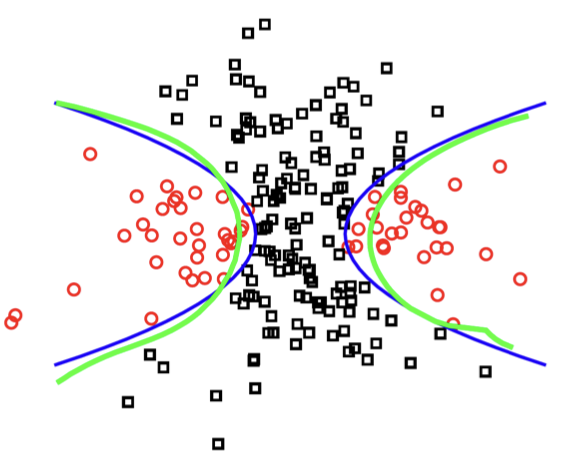
一个核的例子（蓝色：Ground Truth，绿色：学习分类边界）

RBF 核函数

在机器学习中（尤其是支持向量机理论中），径向基函数核（Radial Basis Function Kernel，简称 RBF 核）特指高斯核函数

$$K(\mathbf{x},\mathbf{y})=\exp (-\gamma ||\mathbf{x}-\mathbf{y}|{|}^2)$$

它的特征映射函数为无穷维，其形式为

$$\varphi (\mathbf{x})=\exp (-\gamma ||\mathbf{x}|{|}^2)(1,\sqrt{\frac{2\gamma }{1!}}||\mathbf{x}||,\sqrt{\frac{(2\gamma {)}^2}{2!}}||\mathbf{x}|{|}^2,\cdots ,\sqrt{\frac{(2\gamma {)}^n}{n!}}||\mathbf{x}|{|}^n,\cdots )$$

这是因为

$$\begin{array}{rl}K(\mathbf{x},\mathbf{y})& =\exp (-\gamma ||\mathbf{x}-\mathbf{y}|{|}^2)\\ & =\exp (-\gamma (||\mathbf{x}|{|}^2+||\mathbf{y}|{|}^2-2{\mathbf{x}}^T\mathbf{y}))\\ & =\exp (-\gamma ||\mathbf{x}|{|}^2)\exp (-\gamma ||\mathbf{y}|{|}^2)\exp \left(2\gamma {\mathbf{x}}^T\mathbf{y}\right)\\ & =\exp (-\gamma ||\mathbf{x}|{|}^2)\exp (-\gamma ||\mathbf{y}|{|}^2)\left(\sum _{i=0}^{\mathrm{\infty }}\frac{(2\gamma {\mathbf{x}}^T\mathbf{y}{)}^i}{i!}\right)\\ & ={[\exp (-\gamma ||\mathbf{x}|{|}^2){(\sqrt{\frac{(2\gamma {)}^i}{i!}}||\mathbf{x}|{|}^i)}_{i=0}^{\mathrm{\infty }}]}^T\exp (-\gamma ||\mathbf{y}|{|}^2){(\sqrt{\frac{(2\gamma {)}^i}{i!}}||\mathbf{y}|{|}^i)}_{i=0}^{\mathrm{\infty }}\\ & =⟨\varphi (\mathbf{x}),\varphi (\mathbf{y})⟩\end{array}$$

容易看出，$K$ 的值域是 $(0,1]$，且 $K(\mathbf{x},\mathbf{x})=1$。RBF 核函数有一个参数 $\gamma$，它相当于控制了高斯分布的方差。$\gamma$ 越大，高斯分布的方差越小，模型对于训练数据的拟合程度越高，但是泛化能力会降低；反之，$\gamma$ 减小可以提高泛化能力，但是可能欠拟合。

使用 SciKit-Learn 中的 SVC 类，我们可以通过 kernel='rbf' 来使用 RBF 核函数。

from sklearn.svm import SVC

rbf_svm = SVC(kernel='rbf', C=C, gamma=gamma, random_state=42)
rbf_svm.fit(X_train, y_train)
y_pred = rbf_svm.predict(X_test)

SVC 类构造函数的参数 gamma 控制了高斯核函数的 $\gamma$ 参数，参数 C 是前文软间隔的惩罚系数。