The Pumping Lemma for CFL's

We learned the Pumping Lemma for Regular Languages in previous chapter. It shows that we can have a string in a regular language that can be divided into three parts, whose middle part can be repeated any times. This lemma is very useful in proving regularity. Correspondingly, we have the Pumping Lemma for Context-Free Languages.

The Lemma and Proof

The Lemma is more complicated than the one for regular languages. Its statement is as follows:

For every context-free language $L$, there exists a constant $n$ (the "pumping length") such that for every string $s$ in $L$ of length at least $n$, we can write $s$ as $uvwxy$ such that:

• $|vwx|\le n$
• $|vx|\ge 1$
• For all $i\ge 0$, $u{v}^{i}w{x}^{i}y\in L$

An intuitive explanation is that for every string in a CFL, we can expand one non-terminal symbol $A$ many times and still get a string in the language.

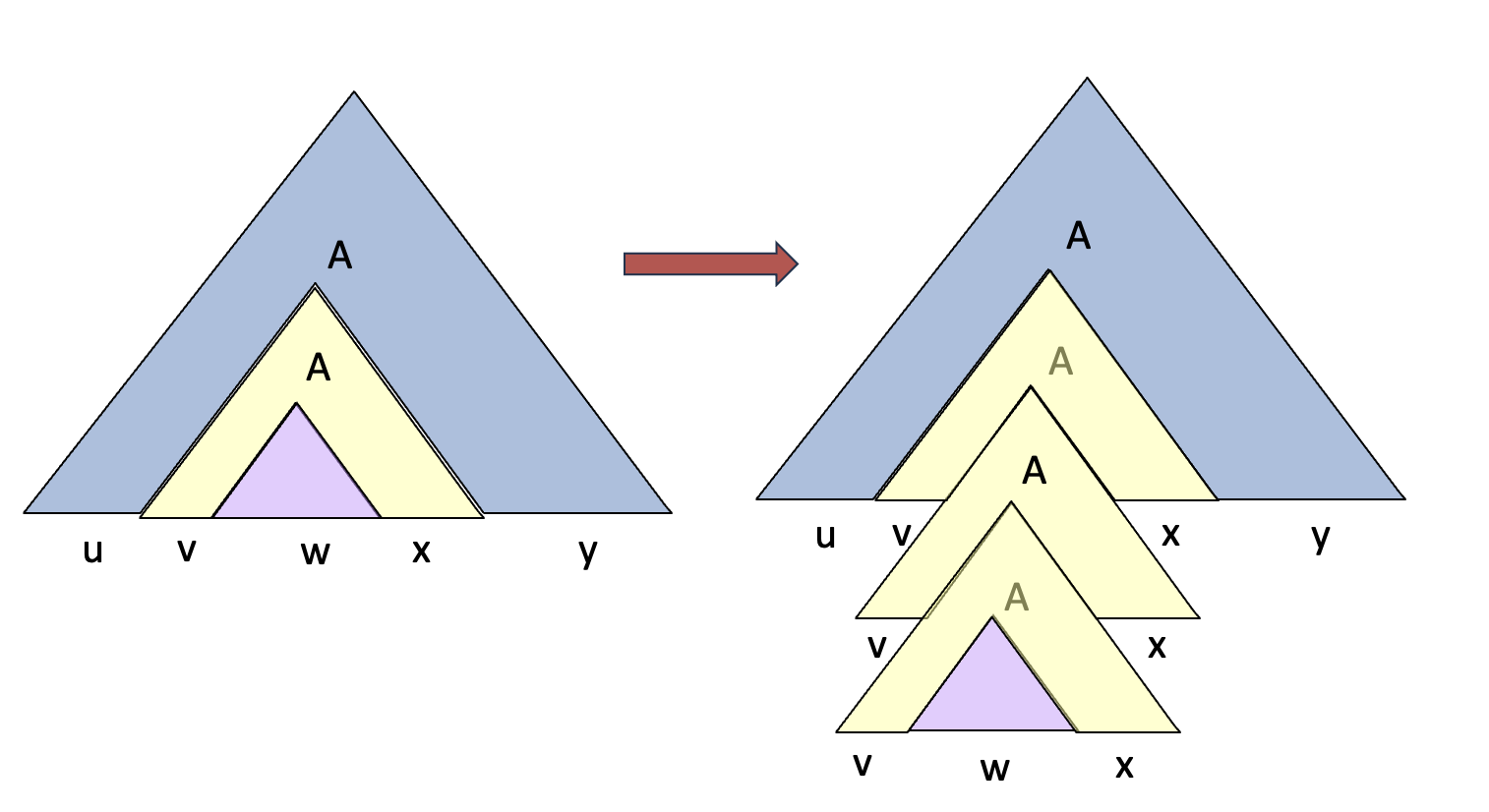
Repeat Production: A intuitive visual perception of the Pumping Lemma

An anticipated question is: How to find the symbol $A$ to expand? Does it even exist? The answer is yes. We can always find a non-terminal symbol to expand. We will show this in the proof.

Proof

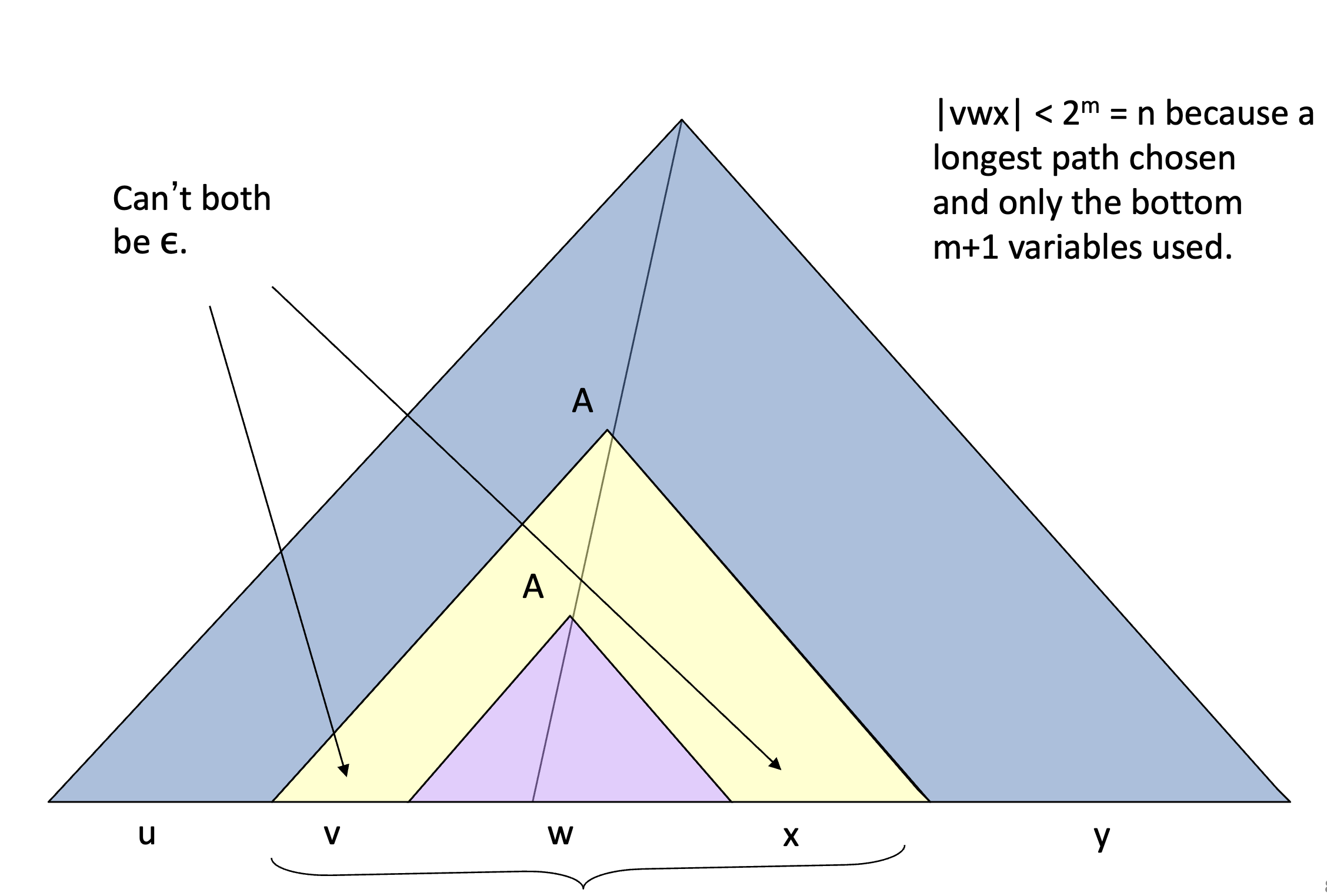
Proof of the Pumping Lemma

We consider a context-free grammar $L-\{\epsilon \}$ in CNF, denote it as $G$. Suppose $G$ has $m$ non-terminal symbols, let $n=2^m$. Then, we make a string $s$ in $L$ of length at least $n$. It can be shown that the parse tree of $s$ has a height of at least $m+2$ (Why?), which means there exists a path of $m+1$ variables in that parse tree. By the Pigeonhole Principle, there must be a non-terminal symbol that appears at least twice in the path, which is the non-terminal symbol $A$ we are trying to find. Apparently, $|vwx|\le 2^m=n$ holds and $|vx|\ge 1$ for there are no $\epsilon$-productions in $G$. We can expand this non-terminal symbol to get plenty of strings in $L$, so for all $i\ge 0$, $u{v}^{i}w{x}^{i}y\in L$. $◻$

Using the Pumping Lemma

Show that the language $L=\{0^i{10}^i{10}^i|i\ge 1\}$ is not context-free.

Proof Suppose $L$ is context-free. Then, by the Pumping Lemma, there exists a constant $n$ such that for every string $s$ in $L$ of length at least $n$.

Consider the string $s=0^n{10}^n{10}^n$, we can write $s$ as $uvwxy$ such that:

• $|vwx|\le n$
• $|vx|\ge 1$

If $vx$ has no $0$'s, then it must have at least one $1$. $uwy$ must have at most one 1, and can't be in $L$. If $vx$ has $0$'s, then $uwy$ has at least one block with $n$ $0$'s and one block with fewer than $n$ $0$'s, which is also impossible to be in $L$. Therefore, $L$ is not context-free. $◻$