Decidability

Decidability is a property of languages. A language is decidable if there exists an algorithm that can determine whether a given string is in the language or not. Apparently, decidable languages are the same as recursive languages.

Inclusion Chain

We have the following inclusion chain of language classes:

$$\text{RL}\subset \text{CFL}\subset \text{Decidable}\subset \text{RE}\subset \text{All Languages}$$

where $\text{RL}$ is the class of regular languages, $\text{CFL}$ is the class of context-free languages, $\text{RE}$ is the class of recursively enumerable languages.

We will show the inclusion and decidability in the following sections.

Do we have non-RE languages?

It seems that the inclusion chain implies that not all languages are recursively enumerable. Indeed, and we will show that there are non-RE languages by constructing one.

Lemma 1: The set of all Turing machines $\text{TM}$ is countable.

Lemma 2: The set of all languages $\text{L}$ is uncountable.

Theorem: There are languages that are not recursively enumerable, for the function $\mathcal{L}:\{\text{TM}\}\to \{\text{L}\}$ cannot be onto.

Proof of Lemma 1: The set of all Turing machines is countable because each Turing machine can be represented by a finite string, and the set of all finite strings is countable (We can easily give a mapping from the set of all finite strings to positive integers).

Proof of Lemma 2: We can use binary string to encode languages, and suppose that the set of all languages is countable, then we can assign one integer to each language and corresponding string. However, we can construct a language

$$L=\{w\mid w\text{ is not in the language encoded by the string }w\}$$

Then, $L$ should have a corresponding integer $i$. If the $i$-th string is in $L$, then it should not in the language encoded by the string $w$, i.e., $L$, and vice versa. This is a contradiction, so the set of all languages is uncountable. $◻$

Lemma 2 can also be proved by Cantor's diagonal argument.

The Halting Problem

The halting problem is the problem of determining, given a description of a program and an input, whether the program will eventually halt when running with that input. Formally, given a pair $⟨M,w⟩$, where $M$ is a Turing machine and $w$ is a string, $\text{HALT}$ is the language of all pairs $⟨M,w⟩$ such that $M$ halts on $w$.

Undecidability

Theorem The halting problem is undecidable.

Proof Suppose that there is a Turing machine $H$ that decides $\text{HALT}$, which takes a pair $⟨M,w⟩$ as input and says yes if $M$ halts on $w$, and no otherwise.

We can define a new Turing machine $H^{\prime }$, which also takes a pair $⟨M,w⟩$ as input. $H^{\prime }$ simulates $H$ on $⟨M,w⟩$ and does the opposite of what $H$ does. That is, if $H$ says yes, then $H^{\prime }$ goes into an infinite loop; if $H$ says no, $H^{\prime }$ halts.

Let's consider what happens when we input $⟨H^{\prime },⟨H^{\prime },w⟩⟩$ to $H^{\prime }$. If $H^{\prime }$ halts, that means the $H$ inside says no, then $H^{\prime }$ should go into an infinite loop. The contradiction also holds when $H^{\prime }$ goes into an infinite loop. Therefore, $H$ and $H^{\prime }$ cannot exist at the same time, which means that the halting problem is undecidable. $◻$

Co-RE Languages

The complement of all recursively enumerable languages is called co-$\text{RE}$ languages. A language $L$ is decidable if and only if $L$ is in both $\text{RE}$ and co-$\text{RE}$. This means:

$$\text{Decidable}=\text{RE}\cap \text{co-RE}$$

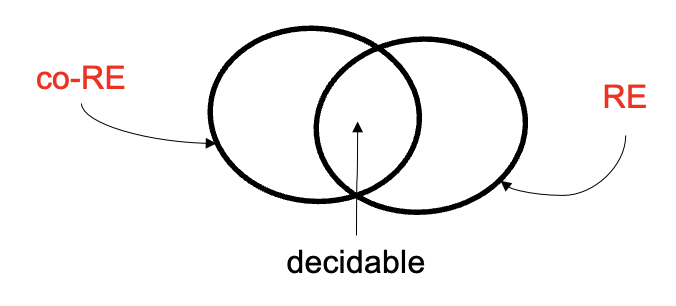
Venn Diagram of RE and co-RE

Proof

We already know that $\text{Decidable}\subset \text{RE}$. If a language is decidable, then its complement is also decidable. So we have $\text{Decidable}\subset \text{co-RE}$.

If a language $L$ is in both $\text{RE}$ and co-$\text{RE}$, then we can construct two Turing machines $T$ and $T^{\prime }$ to recognize the language $L$ and $\overline{L}$, respectively. Then we have a decider just by combining the two Turing machines running in parallel: If $T$ accepts, then accept; if $T^{\prime }$ accepts, then reject.

$◻$

We can easily imply that $\text{HALT}$ is not $\text{RE}$ but co-$\text{RE}$, otherwise $\text{HALT}$ is decidable, which is impossible.